
| 垃圾箱种类垃圾量垃圾种类(吨) | “厨余垃圾”箱 | “可回收物”箱 | “有害垃圾”箱 | “其他垃圾”箱 |
| 厨余垃圾 | 400 | 100 | 40 | 60 |
| 可回收物 | 30 | 140 | 10 | 20 |
| 有害垃圾 | 5 | 20 | 60 | 15 |
| 其他垃圾 | 25 | 15 | 20 | 40 |

| 7 |
| 10 |
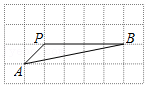
| 3m |
| m2-mn |
| 1 |
| m-n |
| 累计工作时长最多件数(时)种类(件) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 甲类件 | 30 | 55 | 80 | 100 | 115 | 125 | 135 | 145 |
| 乙类件 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
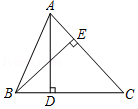
| k |
| x |
| 3 |
| 4 |
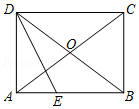
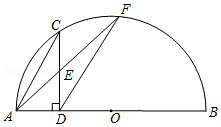
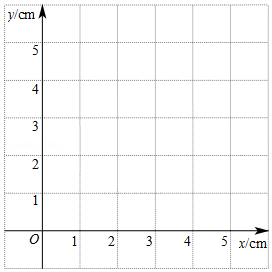
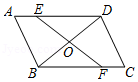
| 位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
| AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
| CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
| FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |