山西省2021年中考考前适应性训练数学试题-乐乐课堂

1．-

的绝对值是(　　)

A. 20
B. -20
C. -
1
20
D.
1
20

2．山西民居砖雕，历史悠久，具有丰富的山西文化内涵，表达了人们对生活的美好祝愿下列砖雕图案中，既是轴对称图形又是中心对称图形的是( )

3．下列运算正确的是(　　)

A. a-2a=a
B. (-a²)³=-a⁶
C. a⁶÷a²=a³
D. (x+y)²=x²+y²

4．2020年12月4日，中国科学技术大学宣布该校潘建伟、陆朝阳等人组成的研究团队成功构建了一台76个光子的量子计算原型机“九章”，问鼎全球最快计算机。它求解数学算法“高斯玻色取样”时，每小时可以处理10亿个样本，则24小时可以处理的样本数用科学记数法表示为( )

A. 2.4×10¹¹个
B. 24×10¹¹个
C. 24×10¹⁰个
D. 2.4×10¹⁰个

5．从-|-6|，-

，-3，0，-

√6

，2π这六个数中随机抽取一个数，恰好为负数的概率为(　　)

A.
2
3
B.
1
6
C.
1
3
D.
1
2

6．将一副三角板按如图方式放置，使EF∥AB，则∠α的度数是(　　)

A. 95°
B. 100°
C. 120°
D. 105°

7．第十六届中国国际文化产业博览交易会以“云上文博会”形式举办，各省通过搭建VR虚拟展馆的形式进行展览，在展会期间，很多有山西地方特色的文化产业发展成果精彩亮相，借此机会，某手工艺术品展台通过网络平台销售了90件上党堆锦圆形摆件，销售情况统计如下表：

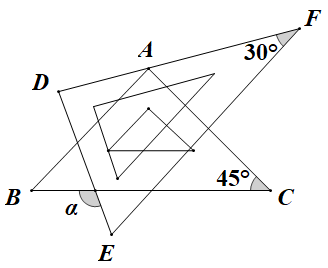
直径(cm)	25	38	48	55	60
销量/件	22	18	30	13	7

则圆形摆件直径的众数为( )

A. 25 cm
B. 30cm
C. 48cm
D. 55cm

8．如图是由六个大小相同的小正方体搭成的几何体的俯视图，则该几何体的左视图不可能是(　　)

9．如图，一次函数y=-x-6的图象经过点P(a，b)和Q(c，d)，则a(c+d)+b(c+d)的值为( )

A. -12
B. -36
C. 36
D. 12

10．如图，在正五边形 ABCDE中，连接AC，BE，BD，AC与BE，BD分别交于点F，G，若AB=2，则FG的长为( )

A. 3-
√5
B.
√5
-1
C.
√5
-1
2
D. 2
√5
-3

11．计算

m•m•…•m

{

9个

n+n+…+n

{

12个

12．若举反例说明命题“若a＜b，则ac＜bc“是假命题时，令a的值为-5，b的值为-2，则可给c取一个具体的值为

13．如图，四边形OABC是正方形，OA在y轴正半轴上，OC在x轴负半轴上．反比例函数y=-

√3

在第二象限的图象与BC，AB分别交于点E，F．若∠EOF=30°，则线段OE的长度为．

14．“闪送”是1小时同城速递服务领域的开拓者和一对一急服务标准的制定者，客户下单后，订单全程只由唯一的“闪送员”专门派送，平均送达时间在60分钟以内，同时避免传统快递服务的中转、分拣，配送过程中存在的诸多安全性问题，某闪送公司每月给闪送员的工资为：底薪1700元，超过300单后另加送单补贴(每送一个包裹称为一单)，送单补贴的具体方案如下：

送单数量	补贴(元/单)
每月超过300单且不超过500单的部分	5
每月超过500单的部分	7

设该月某闪送员送了x单(x＞500)，所得工资为y元，则y与x的函数关系式为．

15．如图，在矩形ABCD中、AB=14，E是BC边上一点，且BE=6，连接AE.若∠CAE=45°，则CE的长为 .

16．(本题共2个小题，第(1)题4分，第(2)题6分，共10分)
(1)解方程：2x²-5x=0；
(2)先化简，再求值：

x−3

x-2

÷(x+2−

x-2

)，其中x=

√2

-3．

17．(本题8分)已知：如图，在△ABC中．

(1)请用直尺和圆规，按以下要求作图(保留作图痕迹).
作法：①作AD平分∠BAC交BC边于点D；
②作线段AD的垂直平分线分别交AB于点E、交AC于点F，
③连接DE、DF．
(2)在(1)所作的图形中，试判断四边形AEDF的形状，并说明理由．

18．(本题9分)走进山西，就如同走进中国历史博物馆，近年来，山西省推出文旅品牌“游山西，读历史”，推动山西文旅走向全国，走向世界，山西文放集团推出五条放游研学线路：

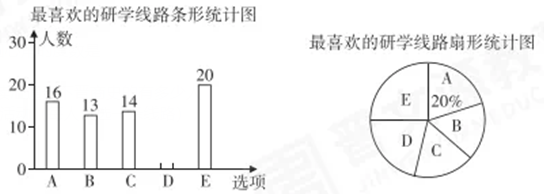
A游山西，读中华文明演进史；
B游山西，读民族融合发展史；
C游山西，读古代建筑艺术史；
D游山西，法汇通天下晋商史；
E游山西，请中国红色革命史；

某校为了了解八年级学生对哪条研学线路最感兴趣，从该校八年级学生中随机抽取若干名学生进行调查，绘制了如图所示的条形统计图和扇形统计图(均不完整)

请根据以上信息，解答下列问题：
(1)本次调查的学生共有名，在扇形统计图中，E所在的圆心角的度数是 °；
(2)将条形统计图补充完整；
(3)若该校八年级共有560名学生，请估计选择“D游山西，读汇通天下晋商史”的有多少人；
(4)小文和小尹作为本校八年级的优秀代表将参加这次研学活动(每人仅选一条线路)，请你用列表或画树状图的方法求他们选择同一条线路的概率.

19．(本题6分)请阅读材料，并完成相应的任务．

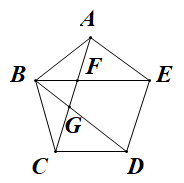
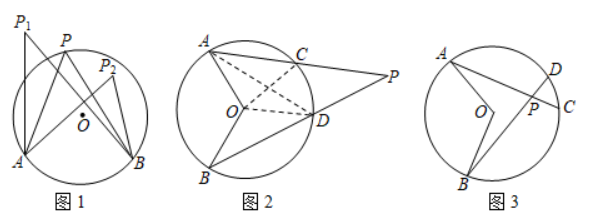
在数学探究课上，同学们在探索与圆有关的角的过程中发现这些角的两边都与圆相交，不断改变顶点的位置，可形成无数个角，而根据点和圆的位置关系可将这些角分为三类，分别是顶点在圆上、圆外和圆内的角，结合数学课上学习的圆周角的概念，对顶点在圆外和圆内的角进行定义：顶点在圆外，两边与圆相交的角叫做圆外角.顶点在圆内，两边都与圆相交的角叫做圆内角，如图1，∠AP₁B和∠AP₂B分别是⌒AB所对的圆外角和圆内角.

如图2，点A，B在⊙O上，∠APB为⌒AB所对的一个圆外角，AP，BP分别交⊙O于点C，D.若∠AOB=120°，⌒CD所对的圆心角为50°，求∠APB.勤奋小组的解题过程(部分)如下：

解：如图2，连接AD，OC，OD.
∵∠ADB是⌒AB所对的圆周角，且∠AOB=120°，
∴∠ADB=

∠AOB=60°.
…

任务
(1)如图1，在探究与圆有关的角时，运用的数学思想方法是：；
A．公理化思想 B．分类讨论 C．数形结合
(2)将勤奋小组的解题过程补充完整；
(3)如图3，当点P在⊙O内时，∠APB是⌒AB所对的一个圆内角，延长AP交⊙O于点C，延长BP交⊙O于点D，若设∠AOB=m°，⌒CD所对的圆心角为n°，则∠APB= °．

20．(本题7分)手机测距APP可以测量物体高度、宽度等，这些测距软件是基于几何学原理设计的测量时只需要输入身高，再用手机拍摄功能将准星对准物体顶端和底部拍摄图片，程序就会计算出物体的高度.某款测距APP提供的测高模式如下：

奋进小组的同学想用上述方式手动计算某景区宣传广告牌的高度.如图2，经过测量得到AB=1.65m，仰角α=35°，俯角β=28°，求出广告牌CD的高度(参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin28°≈0.47，cos28°≈0.88，tan28°=0.53，结果精确到0.1).

21．(本题10分)“居家嗨购，网上过年”，为做好疫情防控并促进春节线上消费，我省组织开展了2021“全晋乐购”网上年货节活动某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工.该企业选购甲、乙两种物品，已知乙种物品单价是甲种物品单价的

，购买9000元甲种物品的数量比购买4800元乙种物品的数量多10件.
(1)甲，乙两种物品的单价各为多少元？
(2)如果该企业购买甲，乙两种物品共150件，总费用不超过3.9万元，则购买甲种物品最多为多少件？

22．（本题12分）综合与实践
问题情境：

如图1，M是线段AB上任意一点（不与点A，B重合），分别以AM和BM为斜边在AB同侧构造等腰直角三角形AMC和等腰直角三角形BMD，连接CD.取AB中点E，CD中点F，连接EF猜想验证：
（1）如图2，当点M与点E重合时，试判断EF与CD之间的数量关系，并说明理由；
延伸探究：
（2）如图3，当点M与点E不重合时，问题（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；
（3）如图3，若AB=2cm，线段EF是否存在最小值，若存在，请直接写出最小值；若不存在，请说明理由.

23．(本题13分)综合与探究
如图1，在平面直角坐标系中，抛物线W₁：y=ax²+bx+3(a≠0)的顶点为A，与y轴交于点D，与x轴交于点B(3，0)，C(-1，0)．P是W₁上的动点，设点P的横坐标为m(0＜m＜3)，过点P作直线l∥x轴．

(1)求抛物线W₁的函数表达式及点A，D的坐标；
(2)如图2，连接BD，直线l交直线BD于点M，连接OP交BD于点N，求PM的长(用含m的代数式表示)及

的最大值；
(3)在点P运动过程中，将抛物线W₁沿直线l对称得到抛物线W₂，W₂与y轴交于点E，F为W₂上一点，试探究是否存在点P，使△DEF是以D为直角顶点的等腰直角三角形？
若存在，直接写出此时点P的坐标；若不存在，请说明理由

查看全部题目

【山西省2021年中考考前适应性训练数学试题】-第1页