24.在一次数学探究活动中,李老师设计了一份活动单:
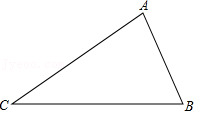
| 已知线段BC=4,使用作图工具作∠BAC=30°,尝试操作后思考:(1)这样的点A唯一吗?(2)点A的位置有什么特征?你有什么感悟? |
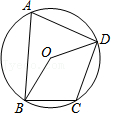
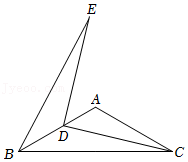
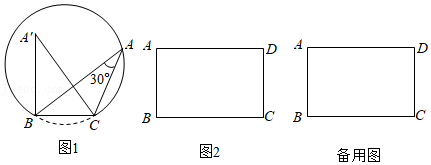
学习小组通过操作、观察、讨论后得到:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外)……小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为
:②△ABC面积的最大值为
;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A',请你利用图1证明∠BA'C>30°;
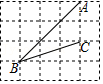
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD的边长为AB=2
√3
,BC=4,点P在直线CD的左侧,且∠DPC=60°.
①线段PB长的最小值为
;②若S
△PCD=
S
△PAD,则线段PD长为
.