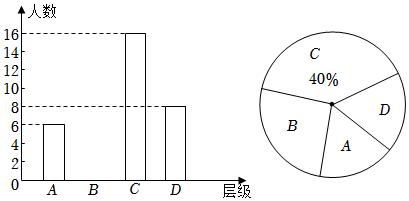
15.根据“五项管理”文件精神,成都某学校优化学校作业管理,探索减负增效新举措,学校就学生做作业时间进行问卷调查,将收集信息进行统计分成A、B、C、D四个层级,其中A:90分钟以上;B:60~90分钟;C:30~60分钟;D:30分钟以下.并将结果绘制成两幅不完整的统计图,请你根据统计信息解答下列问题:
(1)接受问卷调查的学生共有
人;
(2)求扇形统计图中“D”层级的扇形的圆心角度数,并补全条形统计图;
(3)全校约有学生1200人,估计“A”层级的学生约有多少人?
(4)学校从“A”层级的2名女生和2名男生中随机抽取2人参加现场深入调研,请用树形图或列表法求恰好抽到1名男生和1名女生的概率.