| 1 |
| 8 |
| 1 |
| 8 |
 医疗卫生服务机构
医疗卫生服务机构 中国红十字会
中国红十字会 医疗废物
医疗废物 国际急救
国际急救| 7 |
| 5 |
| 1 |
| 2 |
| 1 |
| 8 |
| 8 |
| 3 |
| 8 |
| 15 |
| 152 |
| 45 |
| 44 |
| 15 |
| 5 |
| 6 |
| 25 |
| 26 |
| 15 |
| 13 |
| 5 |
| 13 |
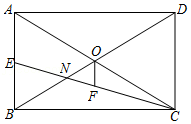
| 2t-1 |
| x |
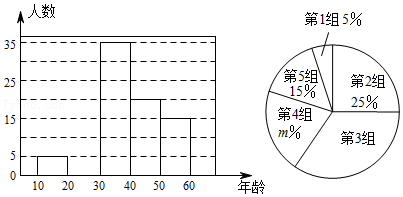
| 组别 | 年龄段 | 频数(人数) |
| 第1组 | 10≤x<20 | 5 |
| 第2组 | 20≤x<30 | a |
| 第3组 | 30≤x<40 | 35 |
| 第4组 | 40≤x<50 | 20 |
| 第5组 | 50≤x<60 | 15 |
| 8x |
| x-2 |
| x+2 |
| 2x-4 |
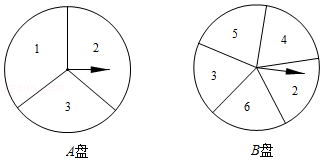
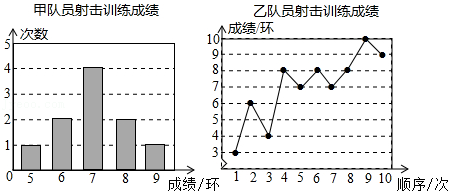
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |
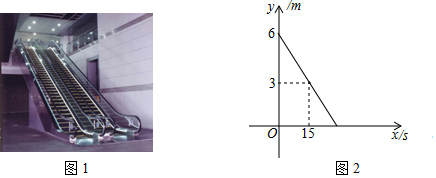
| 售价x(元/件) | 50 | 60 | 70 | 80 |
| 周销售量y(件) | 100 | 80 | 60 | 40 |
| 周销售利润w(元) | 1000 | 1600 | 1800 | 1600 |


| 图案的长度 | 10cm | 20cm | 30cm | 40cm | 50cm | 60cm |
| 所得不同图案的个数 | 1 | 2 | 3 | 5 | 8 | 13 |