19．先化简：(−)÷，然后选择一个合适的x值代入求值．

20．某校“校园主持人大赛”结束后，将所有参赛选手的比赛成绩(得分均为整数)进行整理，并分别绘制成扇形统计图和频数直方图．部分信息如下：

(1)本次比赛参赛选手共有      人，扇形统计图中“79.5～89.5”这一范围的人数占总参赛人数的百分比为      ；
(2)补全图2频数直方图；
(3)赛前规定，成绩由高到低前40%的参赛选手获奖．某参赛选手的比赛成绩为88分，试判断他能否获奖，并说明理由；
(4)成绩前四名是2名男生和2名女生，若从他们中任选2人作为该校文艺晚会的主持人，试求恰好选中1男1女为主持人的概率．

21．如图，无人机在离地面60米的C处，观测楼房顶部B的俯角为30°，观测楼房底部A的俯角为60°，求楼房的高度．

22．如图，点C在以AB为直径的⊙O上，点D是半圆AB的中点，连接AC，BC，AD，BD．过点D作DH∥AB交CB的延长线于点H．
(1)求证：直线DH是⊙O的切线；
(2)若AB=10，BC=6，求AD，BH的长．

23．小刚去超市购买画笔，第一次花60元买了若干支A型画笔，第二次超市推荐了B型画笔，但B型画笔比A型画笔的单价贵2元，他又花100元买了相同支数的B型画笔．
(1)超市B型画笔单价多少元？
(2)小刚使用两种画笔后，决定以后使用B型画笔，但感觉其价格稍贵，和超市沟通后，超市给出以下优惠方案：一次购买不超过20支，则每支B型画笔打九折；若一次购买超过20支，则前20支打九折，超过的部分打八折．设小刚购买的B型画笔x支，购买费用为y元，请写出y关于x的函数关系式．
(3)在(2)的优惠方案下，若小刚计划用270元购买B型画笔，则能购买多少支B型画笔？

24．问题探究：
小红遇到这样一个问题：如图1，△ABC中，AB=6，AC=4，AD是中线，求AD的取值范围．她的做法是：延长AD到E，使DE=AD，连接BE，证明△BED≌△CAD，经过推理和计算使问题得到解决．
请回答：(1)小红证明△BED≌△CAD的判定定理是：      ；
(2)AD的取值范围是      ；
方法运用：
(3)如图2，AD是△ABC的中线，在AD上取一点F，连结BF并延长交AC于点E，使AE=EF，求证：BF=AC．
(4)如图3，在矩形ABCD中，=，在BD上取一点F，以BF为斜边作Rt△BEF，且=，点G是DF的中点，连接EG，CG，求证：EG=CG．

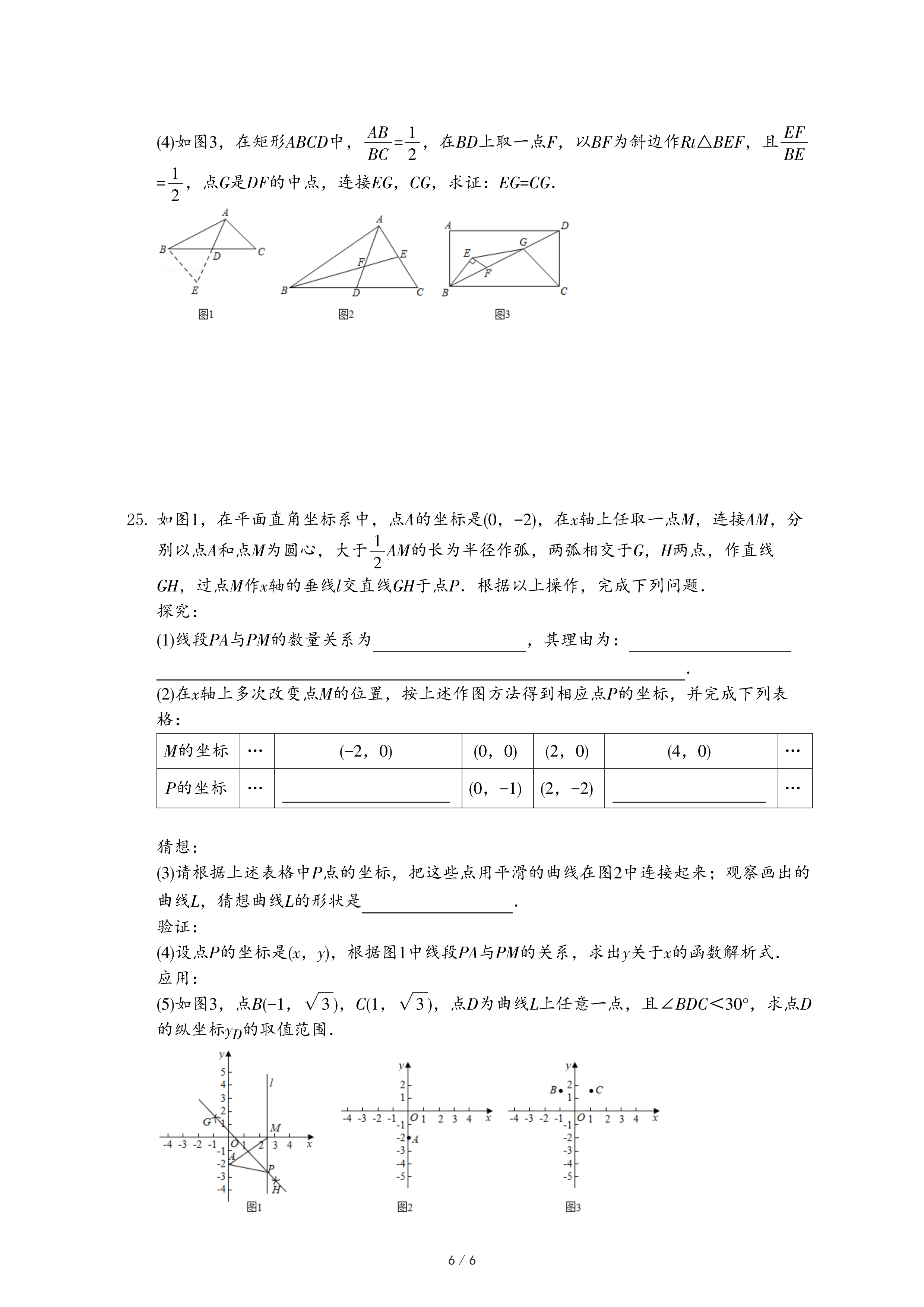
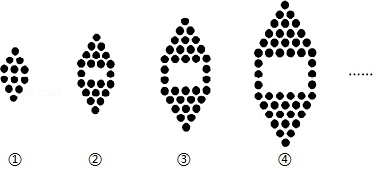
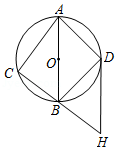
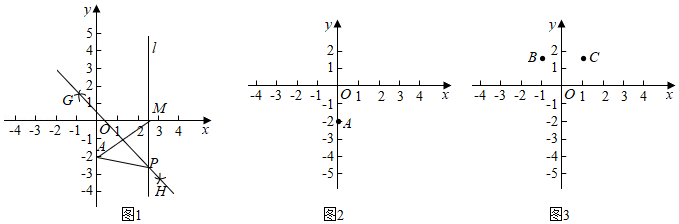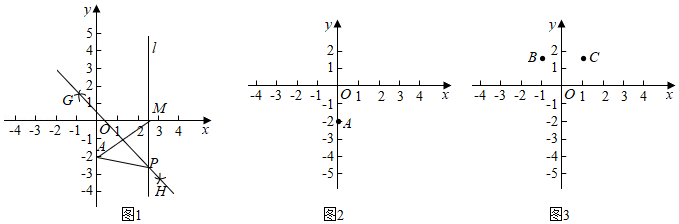25．如图1，在平面直角坐标系中，点A的坐标是(0，-2)，在x轴上任取一点M，连接AM，分别以点A和点M为圆心，大于AM的长为半径作弧，两弧相交于G，H两点，作直线GH，过点M作x轴的垂线l交直线GH于点P．根据以上操作，完成下列问题．
探究：
(1)线段PA与PM的数量关系为      ，其理由为：      ．
(2)在x轴上多次改变点M的位置，按上述作图方法得到相应点P的坐标，并完成下列表格：

猜想：
(3)请根据上述表格中P点的坐标，把这些点用平滑的曲线在图2中连接起来；观察画出的曲线L，猜想曲线L的形状是      ．
验证：
(4)设点P的坐标是(x，y)，根据图1中线段PA与PM的关系，求出y关于x的函数解析式．
应用：
(5)如图3，点B(-1，)，C(1，)，点D为曲线L上任意一点，且∠BDC＜30°，求点D的纵坐标y_D的取值范围．