首页 > 初中试卷 > 九年级试卷 > 九年级数学试卷 > 2019年九年级数学试卷 > 2019年北京九年级数学试卷 > 2019年北京海淀区九年级数学试卷 > 2019年北京海淀区数学中考模拟试卷

2019年北京市海淀区中考数学一模试卷

试卷格式：2019年北京市海淀区中考数学一模试卷.PDF
试卷热词：最新试卷、2019年、北京试卷、海淀区试卷、数学试卷、九年级试卷、中考模拟试卷、初中试卷
如何查看答案以及解析
下载试卷后，用微信扫一扫扫描试卷右上角二维码即可查看【2019年北京市海淀区中考数学一模试卷】解析和视频讲解。
试卷题目
1．如图是圆规示意图，张开的两脚所形成的角大约是(　　)

  • A. 90°
  • B. 60°
  • C. 45°
  • D. 30°
2．若
√x-1
在实数范围内有意义，则实数x的取值范围是(　　)
  • A. x≥1
  • B. x≤1
  • C. x＜1
  • D. x≠1
3．实数a、b、c在数轴上的对应点的位置如图所示，若|a|=|b|，则下列结论中错误的是(　　)

  • A. a+b＞0
  • B. a+c＞0
  • C. b+c＞0
  • D. ac＜0
4．若正多边形的内角和是540°，则该正多边形的一个外角为(　　)
  • A. 45°
  • B. 60°
  • C. 72°
  • D. 90°
5．2019年2月，美国宇航局(NASA)的卫星监测数据显示地球正在变绿，分析发现是中国和印度的行为主导了地球变绿，尽管中国和印度的土地面积加起来只占全球的9%，但过去20年间地球三分之一的新增植被两国贡献的，面积相当于一个亚马逊雨林，已知亚马逊雨林的面积为6560000m2，则过去20年间地球新增植被的面积约为(　　)
  • A. 6.56×106m2
  • B. 6.56×107m2
  • C. 2×107m2
  • D. 2×108m2
6．如果a2-ab-1=0，那么代数式
a2
a-b
⋅(a+
b2-2ab
a
)的值是(　　)
  • A. -1
  • B. 1
  • C. -3
  • D. 3
7．下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化．

根据统计图提供的信息，下列推断合理的是(　　)
  • A. 2018年与2017年相比，我国网约出租车客运量增加了20%以上
  • B. 2018年，我国巡游出租车客运量占出租车客运总量的比例不足60%
  • C. 2015年至2018年，我国出租车客运的总量一直未发生变化
  • D. 2015年至2018年，我国巡游出租车客运量占出租车客运总量的比例逐年增加
8．如图1，一辆汽车从点M外进入路况良好的立交桥，图2反映了它在进入桥区行驶过程中速度(千米/时)与行驶路程(米)之间的关系，根据图2，这辆车的行车路线最有可能是(　　)

  • A.
  • B.
  • C.
  • D.
9．如图为某几何体的展开图，该几何体的名称是      ．

10．如图是北京故宫博物馆2018年国庆期间客流指数统计图(客流指数是指景区当日客流量与2018年10月1日客流量的比值)．

根据图中信息，不考虑其他因素，如果小宇想在今年国庆期间游客较少时参观故宫，最好选择10月      日参观．
11．如图是玉渊潭公园部分景点的分布示意图，在图中，分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系，当表示西桥的点的坐标为(-6，1)，表示中堤桥的点的坐标为(1，2)时，表示留春园的点的坐标为      ．

12．用一组a、b的值说明命题“若a＞b，则a2＞b2”是错误的，这组值可以是a=      ，b=      ．
13．如图，AB是⊙O的直径，C、D为⊙O上的点，若∠CAB=20°，则∠D=      °．

14．如图，在矩形ABCD中，E是边CD的延长线上一点，连接BE交边AD于点F，若AB=4，BC=6，DE=2，则AF的长为      ．

15．2019年2月，全球首个5G火车站在上海虹桥火车站启动，虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍，在峰值速率下传输8千兆数据，5G网络快720秒，求这两种网络的峰值速率，设4G网络的峰值速率为每秒传输x千兆，依题意，可列方程为      ．
16．小宇计划在某外卖网站点如下表所示的菜品，已知每份订单的配送费为3元，商家为了促销，对每份订单的总价(不含配送费)提供满减优惠：满30元减12元，满60元减30元，满100元减45元，如果小宇在购买下表中所有菜品时，采取适当的下订单方式，那么他点餐总费用最低可为      元．
菜品 单价(含包装费) 数量 
水煮牛肉(小) 30元 1 
醋溜土豆丝(小) 12元 1 
豉汁排骨(小) 30元 1 
手撕包菜(小) 12元 1 
米饭 3元 2 

17．计算：4sin60°+(π-1)0-
√12
+|
√3
-1|．
18．解不等式组：
{
5x-1＞2(x+1)
3x+2
4
＞x

19．下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程．

已知：如图1，直线l及直线l外一点P．
求作：直线PQ，使PQ∥l．
作法：如图2，
①在直线l上取一点O，以点O为圆心，OP长为半径画半圆，交直线l于A、B两点；
②连接PA，以B为圆心，AP长为半径画弧，交半圆于点Q；
③作直线PQ；
所有直线PQ就是所求作的直线．
根据小明设计的尺规作图过程．
(1)使用直尺和圆规，补全图形(保留作图痕迹)．
(2)完成下面的证明：
证明：连接PB、QB．
∵PA=QB，
∴⌒PA=      ．
∴∠PBA=∠QPB(      )(填推理的依据)．
∴PQ∥l(      )(填推理的依据)．
20．关于x的一元二次方程ax2+2ax+c=0．
(1)若方程有两个相等的实数根，请比较a、c的大小，并说明理由；
(2)若方程有一个根是0，求此时方程的另一个根．
21．如图，在四边形ABCD中，AB∥CD，AB=BC=2CD，E为对角线AC的中点，F为边BC的中点，连接DE、EF．
(1)求证：四边形CDEF为菱形；
(2)连接DF交AC于点G，若DF=2，CD=
5
3
，求AD的长．

22．如图，AB是⊙O的直径，弦CD⊥AB于点E，在⊙O的切线CM上取一点P，使得∠CPB=∠COA．
(1)求证：PB是⊙O的切线；
(2)若AB=4
√3
，CD=6，求PB的长．

23．在平面直角坐标系xOy中，直线y=2x+b经过点A(1，m)、B(-1，-1)．
(1)求b和m的值；
(2)将点B向右平移到y轴上，得到点C，设点B关于原点的对称点为D，记线段BC与AD组成的图形为G．直接写出点C、D的坐标；
(3)若双曲线y=
k
x
与图形G恰有一个公共点，结合函数图象，求k的取值范围．
24．如图1，线段AB及一定点C、P是线段AB上一动点，作直线CP，过点A作AQ⊥CP于点Q，已知AB=7cm，设A、P两点间的距离为xcm，A、Q两点间的距离为y1cm，P、Q两点间的距离为y2cm．
小明根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
(1)按照下表中自变量x的值进行取点、画图、测量，分别得到了y1、y2与x的几组对应值．
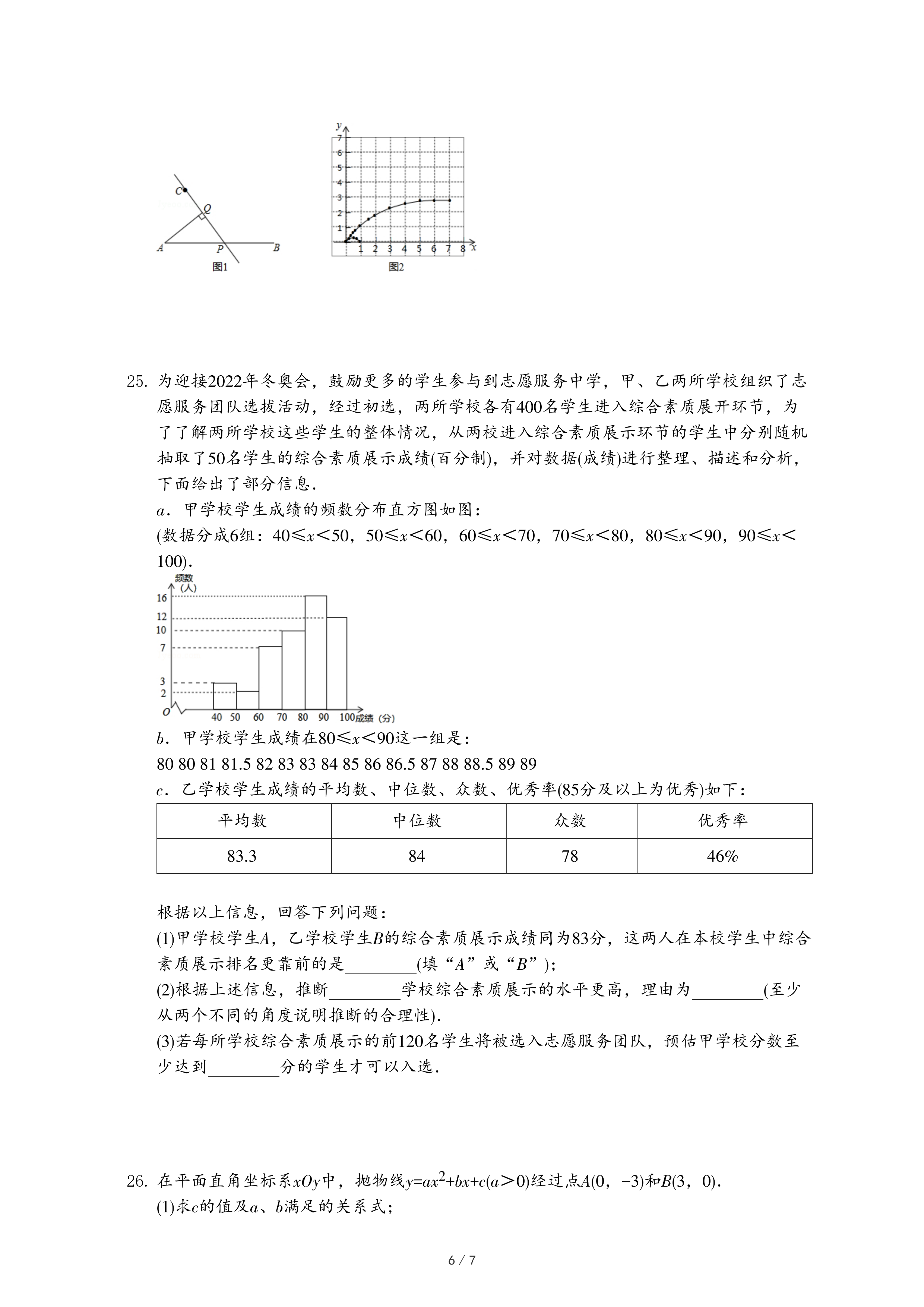
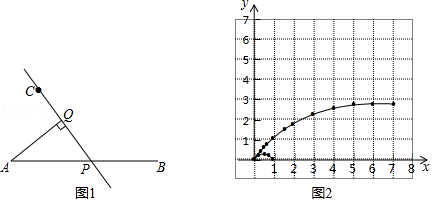
x/cm 0 0.3 0.5 0.8 1 1.5 2 3 4 5 6 7 
y1/cm 0 0.28 0.49 0.79 1 1.48 1.87 2.37 2.61 2.72 2.76 2.78 
y2/cm 0 0.08 0.09 0.06 0 0.29 0.73 1.82        4.20 5.33 6.41 

(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x，y1)，(x，y2)，并画出函数y1，y2的图象；
(3)结合函数图象，解决问题：当△APQ中有一个角为30°时，AP的长度约为      cm．

25．为迎接2022年冬奥会，鼓励更多的学生参与到志愿服务中学，甲、乙两所学校组织了志愿服务团队选拔活动，经过初选，两所学校各有400名学生进入综合素质展开环节，为了了解两所学校这些学生的整体情况，从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制)，并对数据(成绩)进行整理、描述和分析，下面给出了部分信息．
a．甲学校学生成绩的频数分布直方图如图：
(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100)．

b．甲学校学生成绩在80≤x＜90这一组是：
80 80 81 81.5 82 83 83 84 85 86 86.5 87 88 88.5 89 89
c．乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下：
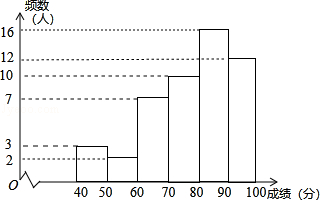
平均数 中位数 众数 优秀率 
83.3 84 78 46% 

根据以上信息，回答下列问题：
(1)甲学校学生A，乙学校学生B的综合素质展示成绩同为83分，这两人在本校学生中综合素质展示排名更靠前的是      (填“A”或“B”)；
(2)根据上述信息，推断      学校综合素质展示的水平更高，理由为      (至少从两个不同的角度说明推断的合理性)．
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队，预估甲学校分数至少达到      分的学生才可以入选．
26．在平面直角坐标系xOy中，抛物线y=ax2+bx+c(a＞0)经过点A(0，-3)和B(3，0)．
(1)求c的值及a、b满足的关系式；
(2)若抛物线在A、B两点间从左到右上升，求a的取值范围；
(3)结合函数图象判断，抛物线能否同时经过点M(-1+m，n)、N(4-m，n)？若能，写出一个符合要求的抛物线的表达式和n的值，若不能，请说明理由．
27．如图，在等腰直角△ABC中，∠ABC=90°，D是线段AC上一点(CA＞2CD)，连接BD，过点C作BD的垂线，交BD的延长线于点E，交BA的延长线于点F．
(1)依题意补全图形；
(2)若∠ACE=α，求∠ABD的大小(用含α的式子表示)；
(3)若点G在线段CF上，CG=BD，连接DG．判断DG与BC的位置关系并证明；
(4)用等式表示DG、CG、AB之间的数量关系为      ．

28．对于平面直角坐标系xOy中的直线l和图形M，给出如下定义：P1、P2、……、Pn-1、Pn是图形M上n(n≥3)个不同的点，记这些点到直线l的距离分别为d1、d2、……、dn-1、dn，若这n个点满足d1+d2+……+dn-1=dn，则称这n个点为图形M关于直线l的一个基准点列，其中dn为该基准点列的基准距离．
(1)当直线l是x轴，图形M上有三点A(-1，1)、B(1，-1)、C(0，2)时，判断A、B、C是否为图形M关于直线l的一个基准点列？如果是，求出它的基准距离；如果不是，请说明理由；
(2)已知直线l是函数y=-
√3
x+3的图象，图形M是圆心在y轴上，半径为1的⊙T，P1、P2、……、Pn-1、Pn是⊙T关于直线l的一个基准点列．若T为原点，求该基准点列的基准距离dn的最大值；
(3)若n的最大值等于6，直接写出圆心T的纵坐标t的取值范围．
查看全部题目
【2019年北京市海淀区中考数学一模试卷】标签
中考模拟试卷 最新试卷 北京试卷 海淀区试卷 2019年试卷 初中试卷 九年级试卷 数学试卷
1 2 3 4 5 6 7 8
下载高清试卷