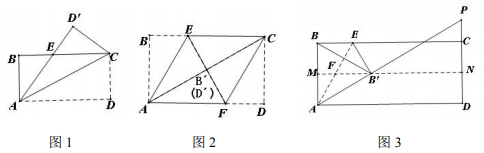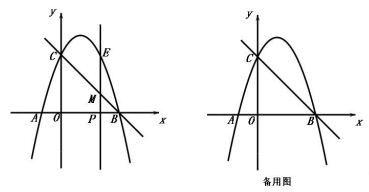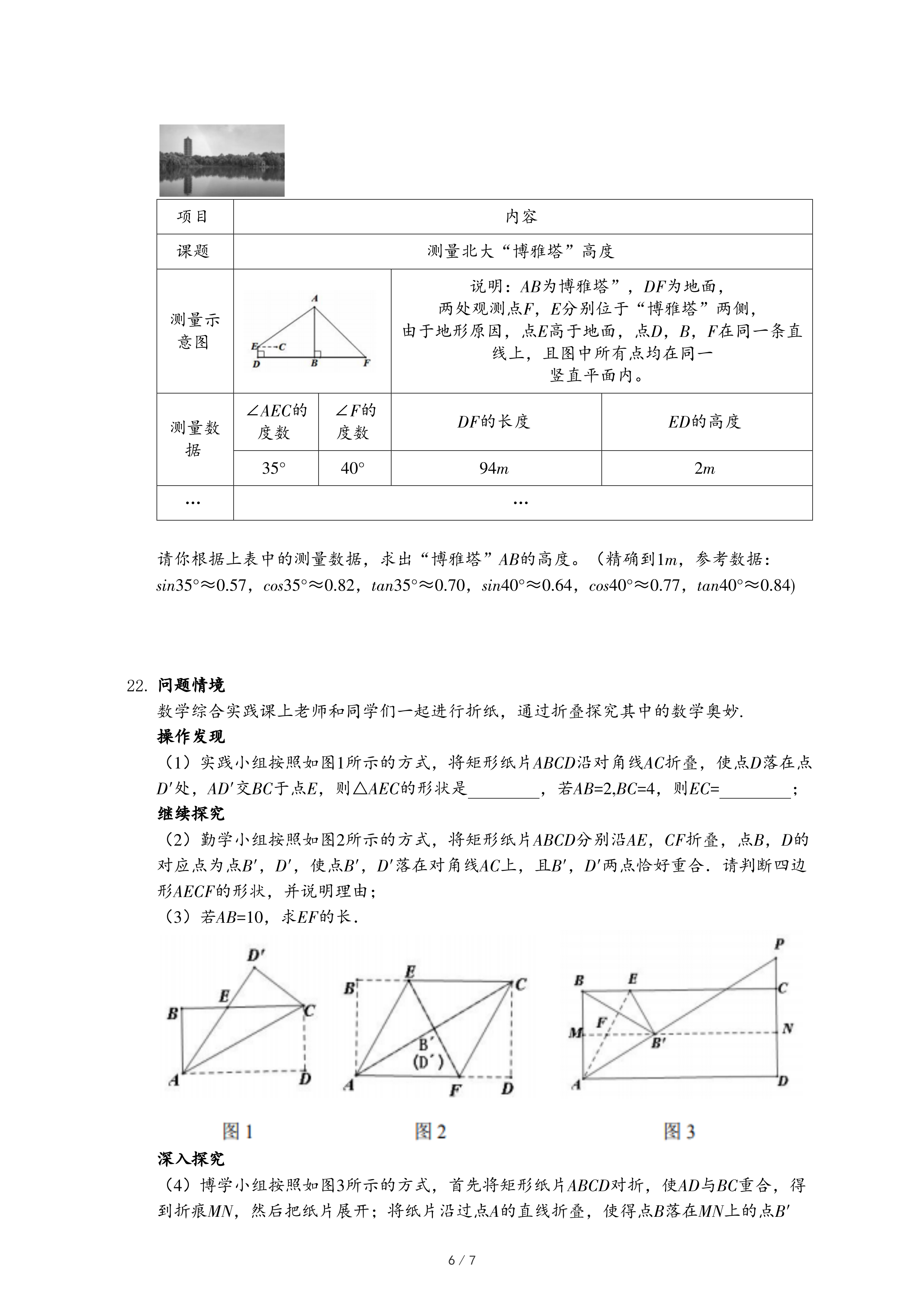



| 1 |
| 2 |
| 1 |
| 2 |

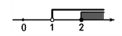
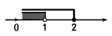
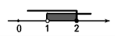
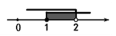
| { | x+1>2 3x-4≤2 |
| { | 9x+11=y 6x+16=y |
| { | 9x−11=y 6x−16=y |
| { | 9x+11=y 6x−16=y |
| { | 9x−11=y 6x+16=y |
| 2-x |
| x-1 |
| x-2 |
| x2-1 |

| 3 |
| 2x+4 |
| 2 |
| x+2 |
| k2 |
| x |
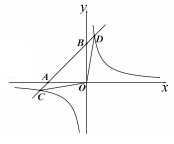
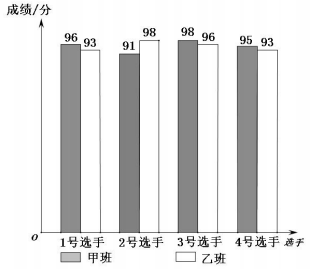
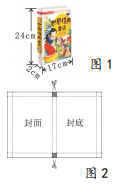
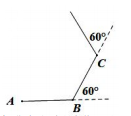
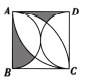
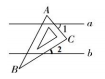
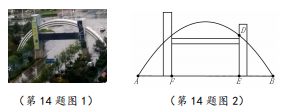
| ×年x月x日星期日 习题积累 1.下面这道题小明的方法和我不同,值得借鉴. 已知:直线l及直线1外一点P. 求作:直线PQ,使得PQ∥l. 小明的作法(如图1): 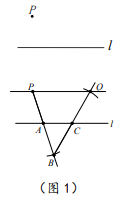 ①在直线l上取一点A,作射线PA,以点A为圆心, AP长为半径作弧,交线段PA的延长线于点B; ②直线l上取一点C(不与点A重合),作射线BC, 以点C为圆心,CB长为半径作弧,交线段BC的 延长线于点Q; ③作直线PQ.则直线PQ就是所求作的直线。 2.下面这道題我不会做,同桌小红给我讲解了作法,但我没弄懂为什么这样做,后来经过小组讨论我才真正明白。 如图2,⊙O是△ABC的外接圆,且AC是⊙O的直径,AB=4,BC=2。 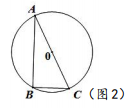 (1)作∠ABC的角平分线BE交⊙O于点E,连接AE; (要求:用尺规作图,保留作图痕迹) (2)求AE的长。 … 【自勉】读书使人头脑充实,讨论使人明辨是非,做笔记则能使知识精确。 ——培根 | |

| 项目 | 内容 | |||
| 课题 | 测量北大“博雅塔”高度 | |||
| 测量示意图 | 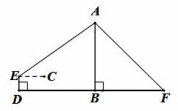 | 说明:AB为博雅塔”,DF为地面, 两处观测点F,E分别位于“博雅塔”两侧, 由于地形原因,点E高于地面,点D,B,F在同一条直线上,且图中所有点均在同一 竖直平面内。 | ||
| 测量数据 | ∠AEC的度数 | ∠F的度数 | DF的长度 | ED的高度 |
| 35° | 40° | 94m | 2m | |
| … | … | |||