


| 1 |
| 2020 |
| 1 |
| 2020 |


| 地市 | 太原 | 大同 | 阳泉 | 晋中 | 吕梁 | 忻州 | 朔州 | 运城 | 临汾 | 长治 | 晋城 |
| 人数(人) | 146 | 152 | 86 | 24 | 34 | 33 | 16 | 143 | 91 | 98 | 109 |

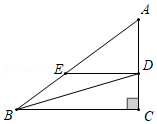
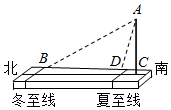
| DE |
| BC |
| 4 |
| 9 |
| AD |
| DC |
| 5 |
| 4 |
√3 π |
| 6 |
√3 |
| 6 |
√3 π |
| 12 |
√3 |
| 12 |
| 4 |
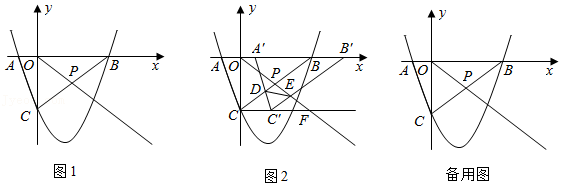
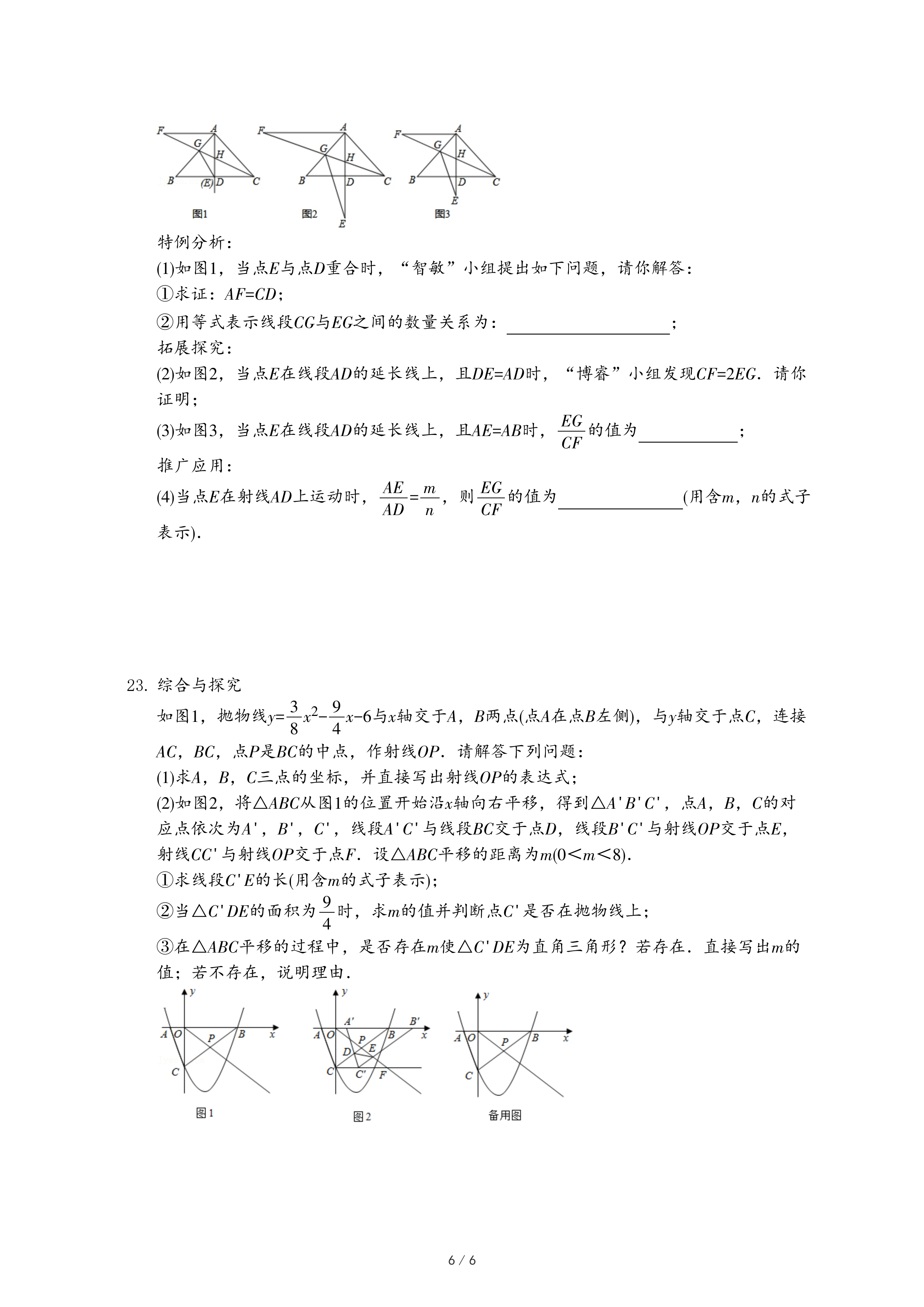
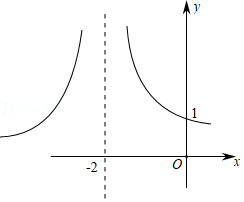
| (x+2)2 |
| 1 |
| 2 |
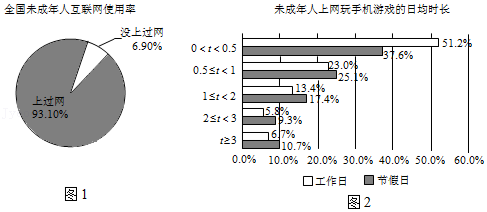
| 项目 | 网上学习 | 听音乐 | 聊天 | 玩游戏 | 搜索信息 |
| 比例 | 92.4% | 77.1% | 73.1% | 64.7% | 55.8% |
| 2 |
| 3 |
| 型号 | A | B |
| 价格 | 8000元/条 | 6000元/条 |

部分分式分解我们知道,将一个多项式转化成若干整式的积的形式,叫做分解因式.分解因式的结果中,每一个因式的次数都低于原来多项式的次数.而有一些特殊的分式可以分解成若干分式的和的形式,我们称之为部分分式分解.例如:将
|
| 8 |
| x2-4x |
| x |
| (x+2)(x-1) |
| M |
| x+2 |
| N |
| x-1 |
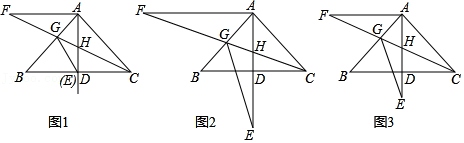
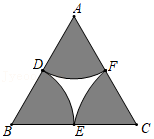
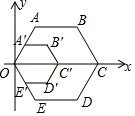
| EG |
| CF |
| AE |
| AD |
| m |
| n |
| EG |
| CF |
| 3 |
| 8 |
| 9 |
| 4 |
| 9 |
| 4 |