2019年山西省阳泉市城区中考数学一模试卷-乐乐课堂

1．计算

2017

×(-2017)的结果是(　　)

A. -2017
B. -1
C. -
1
2017
D. 1

2．下列图形中，是中心对称图形但不是轴对称图形的是(　　)

3．下列事件中，必然事件是(　　)

A.
√6
的值在2到3之间
B. 购买一张彩票一定中奖
C. 任意两个菱形一定是相似图形
D. 打开电视正在播出《人民的名义》

4．如图，等腰直角三角板的顶点A，C分别在直线a，b上．若a∥b，∠1=25°，则∠2的度数为(　　)

A. 10°
B. 15°
C. 20°
D. 25°

5．清明节是中国传统节日，它不仅是人们远足踏青的日子，更是祭奠祖先、缅怀先人的节日．今年4月2日至4日是群众集中祭扫高峰期，我市民政局所属的寝园管理处狮脑山公墓共接待清明祭扫群众67200人，将67200用科学记数法表示应为(　　)

A. 67.2×10³
B. 6.72×10⁴
C. 6.72×10⁵
D. 0.672×10⁵

6．我们在学习“完全平方公式”时，曾通过表示图中几何图形面积的方法进行推导和验证，将抽象的数学知识变得直观，这种方法体现的数学思想是(　　)

A. 数形结合思想
B. 分类思想
C. 转化思想
D. 函数思想

7．如图，点A，B是正方体上的两个顶点，将正方体按图中所示方式展开，则在展开图中B点的位置为(　　)

A. B₁
B. B₂
C. B₃
D. B₄

8．如图，小明将几块六边形纸片分别剪掉了一部分(虚线部分)，得到了一个新多边形．若新多边形的内角和为720°，则对应的图形是(　　)

9．在中国数学名著《九章算术》中，有这样一个问题：“今有共买牛，七家共出一百九十，不足三百三十；九家共出二百七十，盈三十．问家数、牛价各几何？”大意是：几家人凑钱合伙买牛，如果每7家共出190元，那么还缺少330元钱；如果每9家共出270元，又多了30元钱．问共有多少人家，每头牛的价钱是多少元？若设有x户人家，则可列方程为(　　)

A.
190
7
x+330=
270
9
x-30
B.
190
7
x-330=
270
9
x+30
C.
7×190
x
+330=
9×270
x
-30
D.
7×190
x
-330=
9×270
x
+30

10．如图，在平行四边形ABCD中，点E为边DC上一点，且DE：EC=3：1，连接AE并延长，与BC的延长线交于点G，AE与BD交于点F，则△GEC的面积与△DEF的面积之比为(　　)

A. 1：3
B. 3：7
C. 4：21
D. 7：27

11．如图是某品牌4～6岁中童鞋的尺码对照表，设中国码为x，法国码为y，则y与x的函数关系式是．

中童(4～6岁)
中国码	180	185	190	195	200
法国码	26	27	28	29	30
美国码	9	10	11	11.5	12.5

12．五子棋是一种两人对弈的棋类游戏，起源于中国古代的传统黑白棋种，规则是：在正方形棋盘中，由黑方先行，白方后行，轮流弈子，下在棋盘横线与竖线的交叉点上，直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜．如图，这一部分棋盘是两个同学的对弈图．若白子A的坐标为(0，-2)，白子B的坐标为(-2，0)为了不让白方马上获胜，此时黑方应该下在坐标为的位置处．(写出一处即可)

13．不等式组的解集是．

14．在数学课上，老师提出如下问题：
如图，已知线段AB，BC，∠ABC=90°．
求作：矩形ABCD．

小明的作图过程如下：
(1)连接AC，作线段AC的垂直平分线，交AC于M；
(2)连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD．∴四边形ABCD即为所求．

老师说：“小明的作法正确．”
请回答：小明这样作图的依据是．

15．观察下列各式：
①1=1²；②2+3+4=3²；③3+4+5+6+7=5²；④4+5+6+7+8+9+10=7²；…
请你根据观察得到的规律计算：100+101+102+103+…+298= ．

16．(1)计算：(2a²)³+tan60°(

√3

-a⁵)-(

√3

)⁰
(2)解方程：

x-1

x²-1

17．如图，AB是⊙O的直径，C为⊙O上一点，过点C作⊙O的切线DE，AD⊥DE于点D，DE与AB的延长线交于点E，连接AC．
(1)求证：AC平分∠DAE；
(2)若⊙O的半径为2，∠CAB=35°，求⌒BC的长．

18．某校为了了解今年九年级学生的数学学习情况，在中考考前适应性训练测试后，对九年级全体同学的数学成绩作了统计分析，按照成绩高低分为A、B、C、D四个等级并绘制了如图1和图2的统计图(均不完整)，请结合图中所给出的信息解答问题：

(1)该校九年级学生共有人．
(2)补全条形统计图与扇形统计图．(要求：请将扇形统计图的空白部分按比例分成两部分．)

19．根据某网站发布的数据显示，某市二手房均价从今年2月份到4月份连续两次下降，由每平方米4200元下降到每平方米3402元．
(1)求某市2月份到4月份二手房均价平均每次降价的百分率；
(2)假设5月份的均价仍然下降相同的百分率，李明准备购买一套100平方米的二手房，他持有现金15万元，可以在银行贷款20万元，李明的愿望能否实现？

20．请阅读以下材料，并完成相应的任务：
反比例函数图象与三等分角
“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯(Pappus，公元300前后)借助函数给出的一种“三等分锐角”的方法(如图)，步骤如下：
(1)建立直角坐标系，将已知锐角∠AOB的顶点与原点O重合，角的一边OB与x轴正方向重合；
(2)在直角坐标系中，绘制函数y=

的图象，图象与已知角的另一边OA交于点P；
(3)以P为圆心、以2OP为半径作弧，交函数y=

的图象于点R；
(4)分别过点P和R作x轴和y轴的平行线，分别交于点M，点Q；
(5)连接OM得到∠MOB．则∠MOB=

∠AOB．
任务：(1)设P(a，

)，R(b，

)，求直线OM的函数解析式(用含a，b的代数式表示)，并说明Q点在直线OM上；
(2)证明：∠MOB=

∠AOB．

21．小林在使用笔记本电脑时，为了散热，他将电脑放在散热架CAD上，忽略散热架和电脑的厚度，侧面示意图如图1所示，已知电脑显示屏OB与底板OA的夹角为135°，OB=OA=25cm，OE⊥AD于点E，OE=12.5cm．
(1)求∠OAE的度数；
(2)若保持显示屏OB与底板OA的135°夹角不变，将电脑平放在桌面上如图2中的B'O'A所示，则显示屏顶部B'比原来顶部B大约下降了多少？(参考数据：结果精确到0.1cm．参考数据：sin75°≈0.97，cos75°≈0.26，
tan75°≈3.73，

√2

≈1.41，

√3

≈1.73)

22．综合与探究
如图，抛物线y=-x²+bx+c与x轴交于A(-1，0)，B两点，与y轴交于点C，对称轴为x=1．
(1)求抛物线的函数表达式；
(2)在抛物线的对称轴上求一点P，使点P到点A的距离与到点C的距离之和最小，并求出此时点P的坐标；
(3)是否存在过A，B两点的抛物线，其顶点M关于x轴的对称点为N，使得四边形AMBN为正方形？若存在，请直接写出此抛物线的函数表达式；若不存在，请说明理由．

23．综合与实践
问题情境
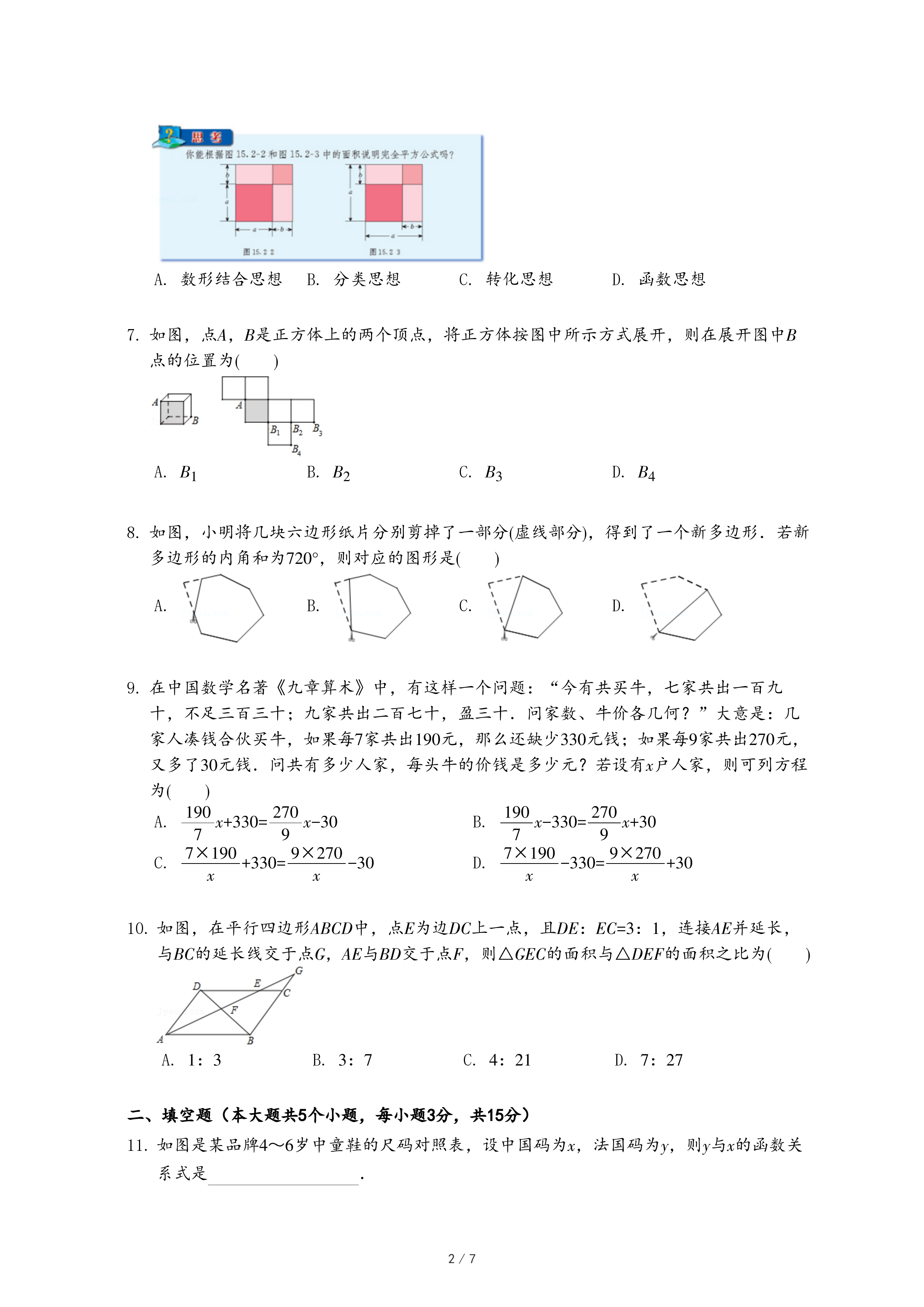
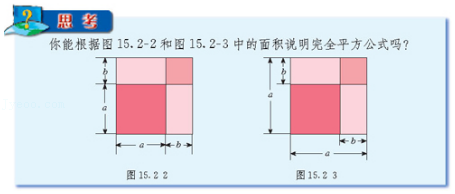
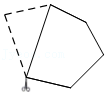
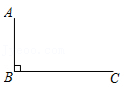
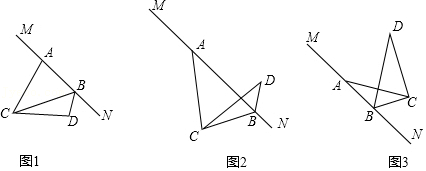
在一节数学活动课上，老师带领同学们借助几何画板对以下题目进行了研究．如图1，MN是过点A的直线，点C为直线MN外一点，连接AC，作∠ACD=60°，使AC=DC，在MN上取一点B，使∠DBN=60°．

观察发现
(1)根据图1中的数据，猜想线段AB、DB、CB之间满足的数量关系是      ；
(2)希望小组认真思考后提出一种证明方法：将CB所在的直线以点C为旋转中心，逆时针旋转60°，与直线MN交于点E，即可证明(1)中的结论．请你在图1中作出线段CE，并根据此方法写出证明过程；
实践探究
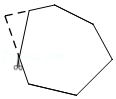
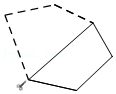
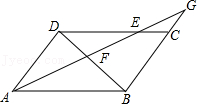
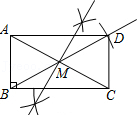
(3)奋进小组在继续探究的过程中，将点C绕点A逆时针旋转，他们发现当旋转到图2和图3的位置时，∠DBN=120°，线段AB、BD、CB的大小发生了变化，但是仍然满足一定的数量关系，请你直接写出这两种关系：
在图2中，线段AB、DB、CB之间满足的数量关系是      ；
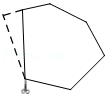
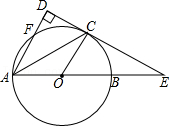
在图3中，线段AB、DB、CB之间满足的数量关系是      ；
提出问题
(4)智慧小组提出一个问题：若图3中BC⊥CD于点C时，BC=2，则AC为多长？请你解答此问题．

查看全部题目