25.为进一步增强中小学生“知危险会避险”的意识,某校初三年级开展了系列交通安全知识竞赛,从中随机抽取30名学生两次知识竞赛的成绩(百分制),并对数据(成绩)进行收集、整理、描述和分析.下面给出了部分信息.
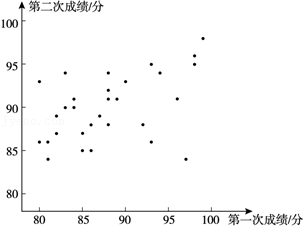
a.这30名学生第一次竞赛成绩和第二次竞赛成绩得分情况统计图:
b.下表是这30名学生两次知识竞赛的获奖情况相关统计:
| | 参与奖 | 优秀奖 | 卓越奖 |
| 第一次竞赛 | 人数 | 10 | 10 | 10 |
| 平均分 | 82 | 87 | 95 |
| 第二次竞赛 | 人数 | 2 | 12 | 16 |
| 平均分 | 84 | 87 | 93 |
(规定:分数≥90,获卓越奖;85≤分数<90,获优秀奖;分数<85,获参与奖)
c.第二次竞赛获卓越奖的学生成绩如下:
90 90 91 91 91 91 92 93 93 94 94 94 95 95 96 98
d.两次竞赛成绩样本数据的平均数、中位数、众数如表:
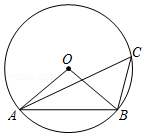
| | 平均数 | 中位数 | 众数 |
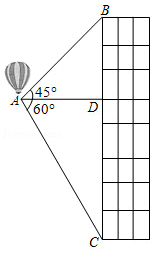
| 第一次竞赛 | m | 87.5 | 88 |
| 第二次竞赛 | 90 | n | 91 |
根据以上信息,回答下列问题:
(1)小松同学第一次竞赛成绩是89分,第二次竞赛成绩是91分,在图中用“〇”圈出代表小松同学的点;
(2)直接写出m,n的值;
(3)可以推断出第
次竞赛中初三年级全体学生的成绩水平较高,理由是
.