25.2021年7月1日是中国共产党成立100周年纪念日.为了让全校学生牢固树立爱国爱党的崇高信念,某校开展了形式多样的党史学习教育活动.八、九年级各300名学生举行了一次党史知识竞赛(百分制),然后随机抽取了八、九年级各20名学生的成绩进行了整理与分析,部分信息如下:
a.抽取九年级20名学生的成绩如表:
| 86 | 88 | 97 | 91 | 94 | 62 | 51 | 94 | 87 | 71 |
| 94 | 78 | 92 | 55 | 97 | 92 | 94 | 94 | 85 | 98 |
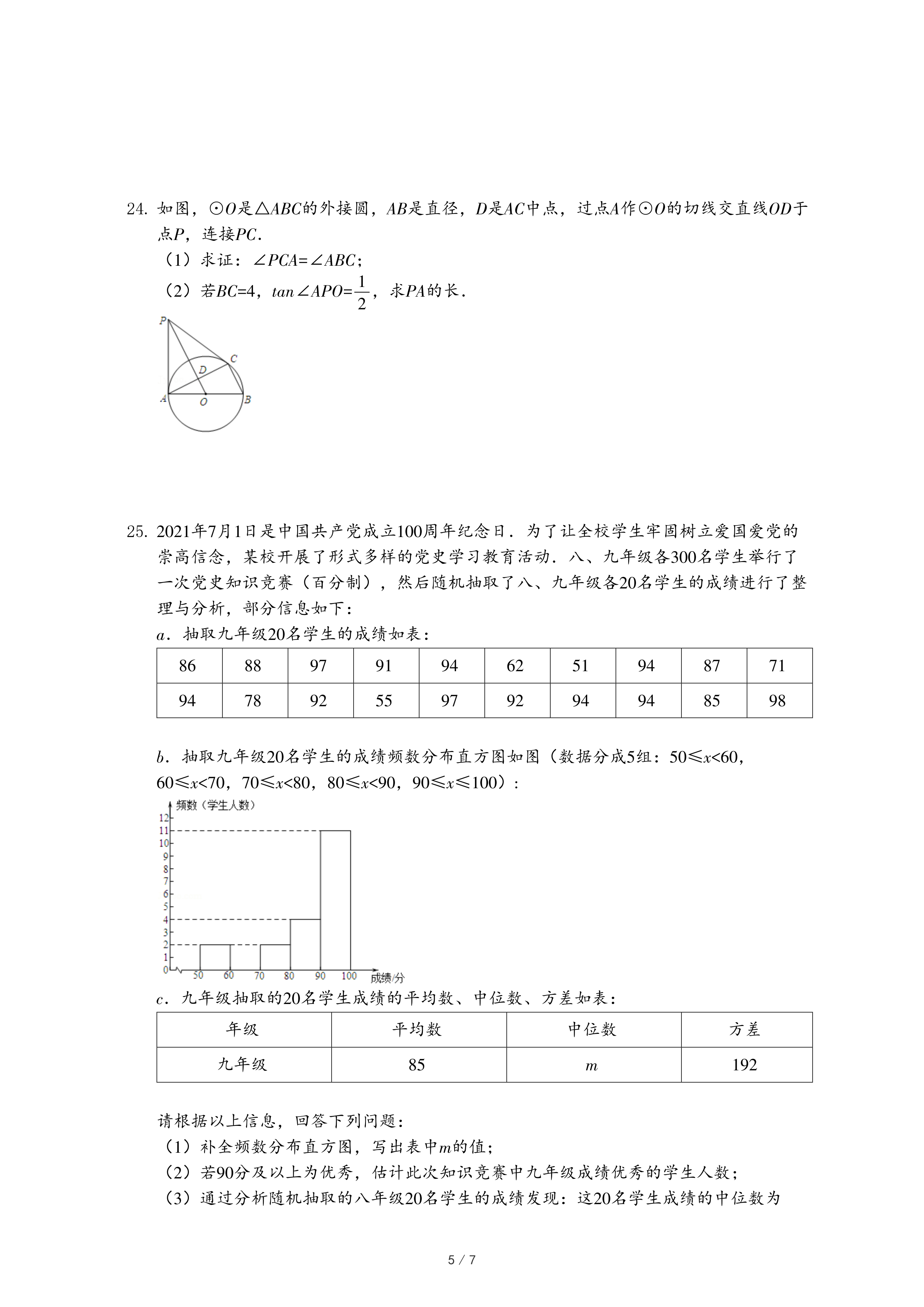
b.抽取九年级20名学生的成绩频数分布直方图如图(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

c.九年级抽取的20名学生成绩的平均数、中位数、方差如表:
| 年级 | 平均数 | 中位数 | 方差 |
| 九年级 | 85 | m | 192 |
请根据以上信息,回答下列问题:
(1)补全频数分布直方图,写出表中m的值;
(2)若90分及以上为优秀,估计此次知识竞赛中九年级成绩优秀的学生人数;
(3)通过分析随机抽取的八年级20名学生的成绩发现:这20名学生成绩的中位数为88,方差为80.4,且八、九两个年级随机抽取的共40名学生成绩的平均数是85.2.
①求八年级这20名学生成绩的平均数;
②你认为哪个年级的成绩较好,说明理由(至少从两个不同的角度说明推断的合理性).



 禁止驶入
禁止驶入 靠左侧道路行驶
靠左侧道路行驶 向左和向右转弯
向左和向右转弯 环岛行驶
环岛行驶