首页 > 初中试卷 > 九年级试卷 > 九年级数学试卷 > 2019年九年级数学试卷 > 2019年北京九年级数学试卷 > 2019年北京数学中考模拟试卷

【2019年北京市石景山区中考数学二模试卷】-第2页

试卷格式：2019年北京市石景山区中考数学二模试卷.PDF
试卷热词：最新试卷、2019年、北京试卷、数学试卷、九年级试卷、中考模拟试卷、初中试卷
如何查看答案以及解析
下载试卷后，用微信扫一扫扫描试卷右上角二维码即可查看【2019年北京市石景山区中考数学二模试卷】解析和视频讲解。
试卷题目
1．如图所示在△ABC中，AB边上的高线画法正确的是(　　)
  • A.
  • B.
  • C.
  • D.
2．下列各式计算正确的是(　　)
  • A. x2•x3=x5
  • B. x2+3x2=4x4
  • C. x8÷x2=x4
  • D. (3x2y)2=6x4y2
3．如图是某几何体的展开图．则该几何体是(　　)

  • A. 三棱柱
  • B. 四棱柱
  • C. 三棱锥
  • D. 四棱锥
4．不等式-
x
2
＞2的解集在数轴上的表示正确的是(　　)
  • A.
  • B.
  • C.
  • D.
5．如图，在▱ABCD中，AC=8，BD=6，AD=5，则▱ABCD的面积为(　　)

  • A. 6
  • B. 12
  • C. 24
  • D. 48
6．如图，AB是⊙O的弦，直径CD交AB于点E，若AE=EB=3，∠C=15°，则OE的长为(　　)

  • A.
    √3
  • B. 4
  • C. 6
  • D. 3
    √3

7．为了迎接2022年的冬奥会，中小学都积极开展冰上运动，小乙和小丁进行500米短道速滑比赛，他们的五次成绩(单位：秒)如表所示：
 1 2 3 4 5 
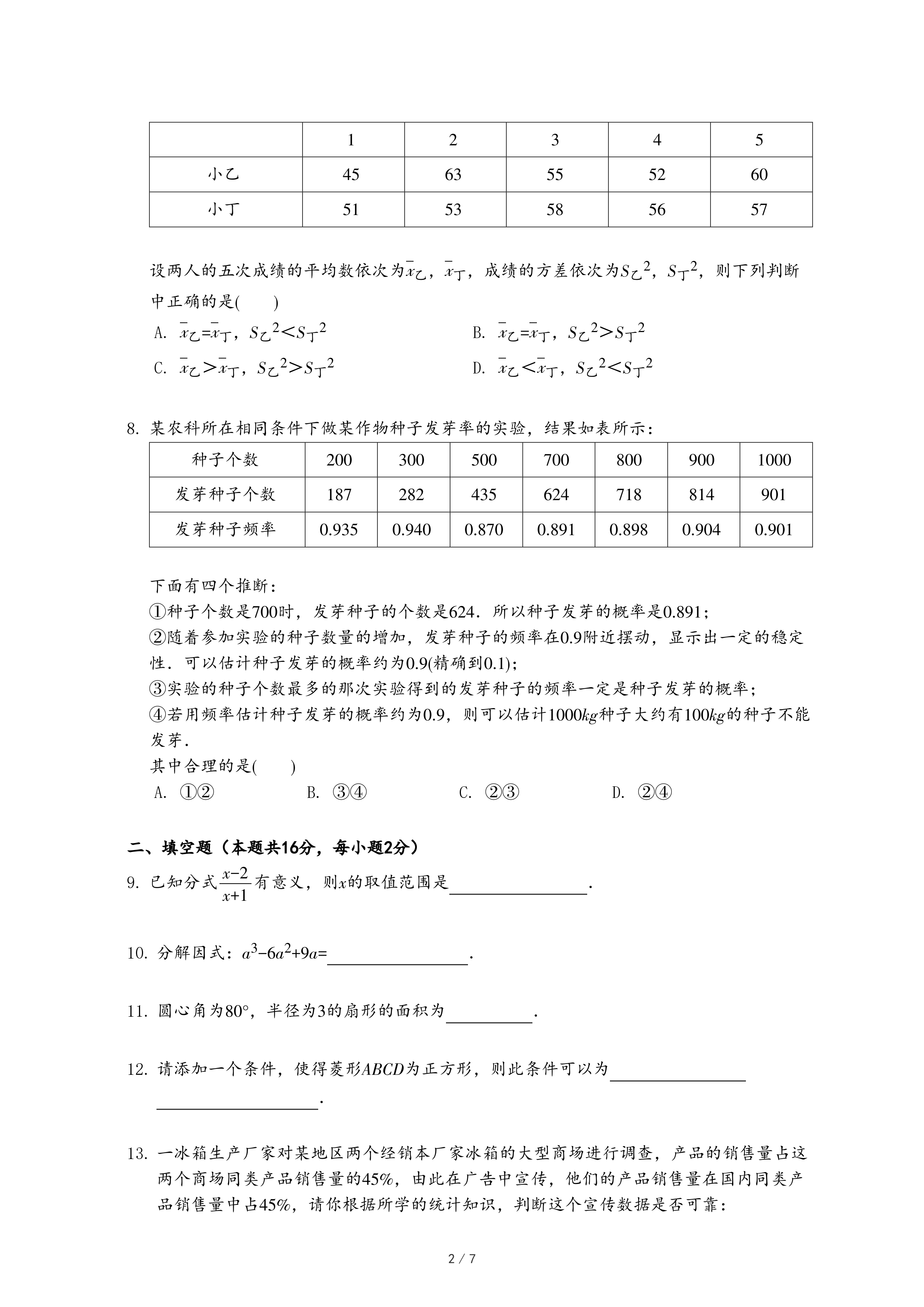
小乙 45 63 55 52 60 
小丁 51 53 58 56 57 

设两人的五次成绩的平均数依次为x乙，x丁，成绩的方差依次为S乙2，S丁2，则下列判断中正确的是(　　)
  • A. x乙=x丁，S乙2＜S丁2
  • B. x乙=x丁，S乙2＞S丁2
  • C. x乙＞x丁，S乙2＞S丁2
  • D. x乙＜x丁，S乙2＜S丁2
8．某农科所在相同条件下做某作物种子发芽率的实验，结果如表所示：
种子个数 200 300 500 700 800 900 1000 
发芽种子个数 187 282 435 624 718 814 901 
发芽种子频率 0.935 0.940 0.870 0.891 0.898 0.904 0.901 

下面有四个推断：
①种子个数是700时，发芽种子的个数是624．所以种子发芽的概率是0.891；
②随着参加实验的种子数量的增加，发芽种子的频率在0.9附近摆动，显示出一定的稳定性．可以估计种子发芽的概率约为0.9(精确到0.1)；
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率；
④若用频率估计种子发芽的概率约为0.9，则可以估计1000kg种子大约有100kg的种子不能发芽．
其中合理的是(　　)
  • A. ①②
  • B. ③④
  • C. ②③
  • D. ②④
9．已知分式
x-2
x+1
有意义，则x的取值范围是      ．
10．分解因式：a3-6a2+9a=      ．
11．圆心角为80°，半径为3的扇形的面积为      ．
12．请添加一个条件，使得菱形ABCD为正方形，则此条件可以为      ．
13．一冰箱生产厂家对某地区两个经销本厂家冰箱的大型商场进行调查，产品的销售量占这两个商场同类产品销售量的45%，由此在广告中宣传，他们的产品销售量在国内同类产品销售量中占45%，请你根据所学的统计知识，判断这个宣传数据是否可靠：      (填是或否)，理由是      ．
14．如图，正方形ABCD，E是AD上一点，AE=
1
3
AD=1，CF⊥BE于F，则BF的长为      ．

15．如图，在喷水池的中心A处竖直安装一个水管AB，水管的顶端安有一个喷水池，使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C，高度为3m，水柱落地点D离池中心A处3m，以水平方向为x轴，建立平面直角坐标系，若选取A点为坐标原点时的抛物线的表达式为y=-
3
4
(x-1)2+3(0≤x≤3)，则选取点D为坐标原点时的抛物线表达式为      ，水管AB的长为      m．

16．北京世界园艺博览会(简称“世园会”)园区4月29日正式开园，门票价格如下：
票种 票价(元/人) 
指定日 普通票 160 
优惠票 100 
平日 普通票 120 
优惠票 80 

注1：“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日)，“平日”为世园会会期除“指定日”外的其他日期；
注2：六十周岁及以上老人、十八周岁以下的学生均可购买优惠票；
注3：提前两天及以上在线上购买世园会门票，票价可打九折，但仅限于普通票．
某大家庭计划在6月1日集体入园参观游览，通过计算发现：若提前两天线上购票所需费用为996元，而入园当天购票所需费用为1080元，则该家庭中可以购买优惠票的有      人．
17．下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程．
已知：∠AOB．
求作：∠APC，使得∠APC=2∠AOB．
作法：如图，
①在射线OB上任取一点C；
②作线段OC的垂直平分线，交OA于点P，交OB于点D；
③连接PC；
所以∠APC即为所求作的角．
根据小华设计的尺规作图过程，
(1)使用直尺和圆规补全图形(保留作图痕迹)；
(2)完成下面的证明(说明：括号里填写推理的依据)．
证明：∵DP是线段OC的垂直平分线，
∴OP=      (      )
∴∠O=∠PCO．
∵∠APC=∠O+∠PCO(      )
∴∠APC=2∠AOB．

18．计算：
√3
tan60°-
3√8
-(-2)-2+|-
√2
|
19．已知y2-2xy-1=0，求代数式(x-2y)2-(x-y)(x+y)-3y2的值．
20．已知关于x的一元二次方程(m-2)x2+3x-1=0有两个不相等的实数根．
(1)求m的取值范围；
(2)若方程的两个根都是有理数，请选择一个合适的m，并求出此方程的根．
21．如图，AB平分∠CAD，∠ACB+∠ADB=180°，
(1)求证：BC=BD
(2)若BD=10，cos∠ADB=
2
5
，求AD-AC的值．

22．如图，在Rt△ABC中，∠C=90°，点O在边AC上，⊙O与边AC相交于点D、与边AB相切于点E，过点D作DP∥BC交AB于点P．
(1)求证：PD=PE；
(2)连接CP，若点E是AP的中点，OD：DC=2：1，CP=13，求⊙O的半径．

23．在平面直角坐标系xOy中，A(-3，2)，B(0，1)，将线段AB沿x轴的正方向平移n(n＞0)个单位，得到线段A′，B′恰好都落在反比例函数y=
m
x
(m≠0)的图象上．
(1)用含n的代数式表示点A′，B′的坐标；
(2)求n的值和反比例函数y=
m
x
(m≠0)的表达式；
(3)点C为反比例函数y=
m
x
(m≠0)图象上的一个动点，直线CA′与x轴交于点D，若CD=2A′D，请直接写出点C的坐标．
24．如图，P是矩形ABCD内部的一定点，M是AB边上一动点，连接MP并延长与矩形ABCD的一边交于点N，连接AN．已知AB=6cm，设A，M两点间的距离为xcm，M，N两点间的距离为y1cm，A，N两点间的距离为y2cm．小欣根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小欣的探究过程，请补充完整；
(1)按照如表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；
x/cm 0 1 2 3 4 5 6 
y1/cm 6.30 5.40        4.22 3.13 3.25 4.52 
y2/cm 6.30 6.34 6.43 6.69 5.75 4.81 3.98 

(2)在同一平面直角坐标系xOy中，描出以补全后的表中各组对应值所对应的点(x，y1)，并画出函数y1的图象；
(3)结合函数图象，解决问题：当△AMN为等腰三角形时，AM的长度约为      cm．

25．为了响应全民阅读的号召，某社区开展了为期一年的“读书伴我行”阅读活动，在阅读活动开展之初，随机抽取若干名社区居民，对其年阅读量(单位：本)进行了调查统计与分析，结果如下：
平均数 中位数 众数 最大值 最小值 方差 
6.9 7.5 8 16 1 18.69 

经过一年的“读书伴我行”阅读活动，某社区再次对这部分居民的年阅读量进行调查，并对收集的数据进行了整理、描述和分析，下面给出了部分信息．
a．居民的年阅读量统计表如下：
阅读量 2 4 5 8 9 10 11 12 13 16 21 
人数 5 5 5 3 2 m 5 5 3 7 n 

b．分组整理后的居民阅读量统计表、统计图如下：
组别 阅读量/本 频数 
A 1≤x＜6 15 
B 6≤x＜11   
C 11≤x＜16 13 
D 16≤x≤21   

c．居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下：
平均数 中位数 众数 最大值 最小值 方差 
10.4 10.5 q 21 2 30.83 

根据以上信息，回答下列问题：
(1)样本容量为      ；
(2)m=      ；p=      ；q=      ；
(3)根据社区开展“读书伴我行”阅读活动前、后随机抽取的部分居民阅读量的两组调查结果，请至少从两个方面对社区开展阅读活动的效果进行评价．

26．在平面直角坐标系xOy中，已知抛物线y=x2-2mx+m2-1
(1)求抛物线的对称轴(用含m的式子去表示)；
(2)若点(m-2，y1)，(m，y2)，(m+3，y3)都在抛物线y=x2-2mx+m2-1上，则y1、y2、y3的大小关系为      ；
(3)直线y=-x+b与x轴交于点A(3，0)，与y轴交于点B，过点B作垂直于y轴的直线l与抛物线y=x2-2mx+m2-1有两个交点，在抛物线对称轴右侧的点记为P，当△OAP为钝角三角形时，求m的取值范围．
27．如图在△ABC中，∠ACB=90°，AC=BC，E为外角∠BCD平分线上一动点(不与点C重合)，点E关于直线BC的对称点为F，连接BE，连接AF并延长交直线BE于点G．
(1)求证：AF=BE；
(2)用等式表示线段FG，EG与CE的数量关系，并证明．

28．对于平面直角坐标系xOy中的点P，Q，给出如下定义：若P，Q为某个三角形的顶点，且边PQ上的高h，满足h=PQ，则称该三角形为点P，Q的“生成三角形”．
(1)已知点A(4，0)；
①若以线段OA为底的某等腰三角形恰好是点O，A的“生成三角形”，求该三角形的腰长；
②若Rt△ABC是点A，B的“生成三角形”，且点B在x轴上，点C在直线y=2x-5上，则点B的坐标为      ；
(2)⊙T的圆心为点T(2，0)，半径为2，点M的坐标为(2，6)，N为直线y=x+4上一点，若存在Rt△MND，是点M，N的“生成三角形”，且边ND与⊙T有公共点，直接写出点N的横坐标xN的取值范围．
查看全部题目
【2019年北京市石景山区中考数学二模试卷】标签
中考模拟试卷 最新试卷 北京试卷 2019年试卷 初中试卷 九年级试卷 数学试卷
1 2 3 4 5 6 7 8
下载高清试卷