24.截止到2020年11月,我国贫困县“摘帽”计划已经全部完成,脱贫攻坚取得了全面胜利!为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对各省贫困地区的持续投入.小凯同学通过登陆国家乡村振兴局网站,查询到了2020年中央财政脱贫专项资金对我国28个省、直辖市、自治区的分配额度(亿元),并对数据进行整理,描述和分析.下面是小凯给出的部分信息.
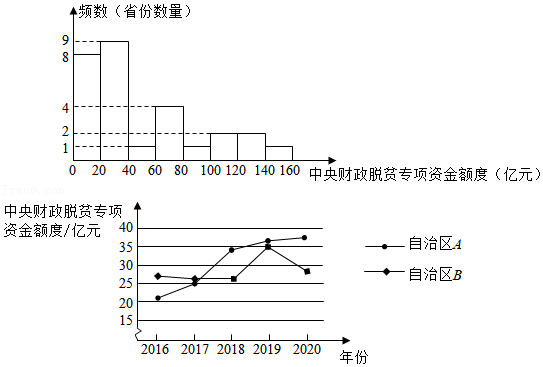
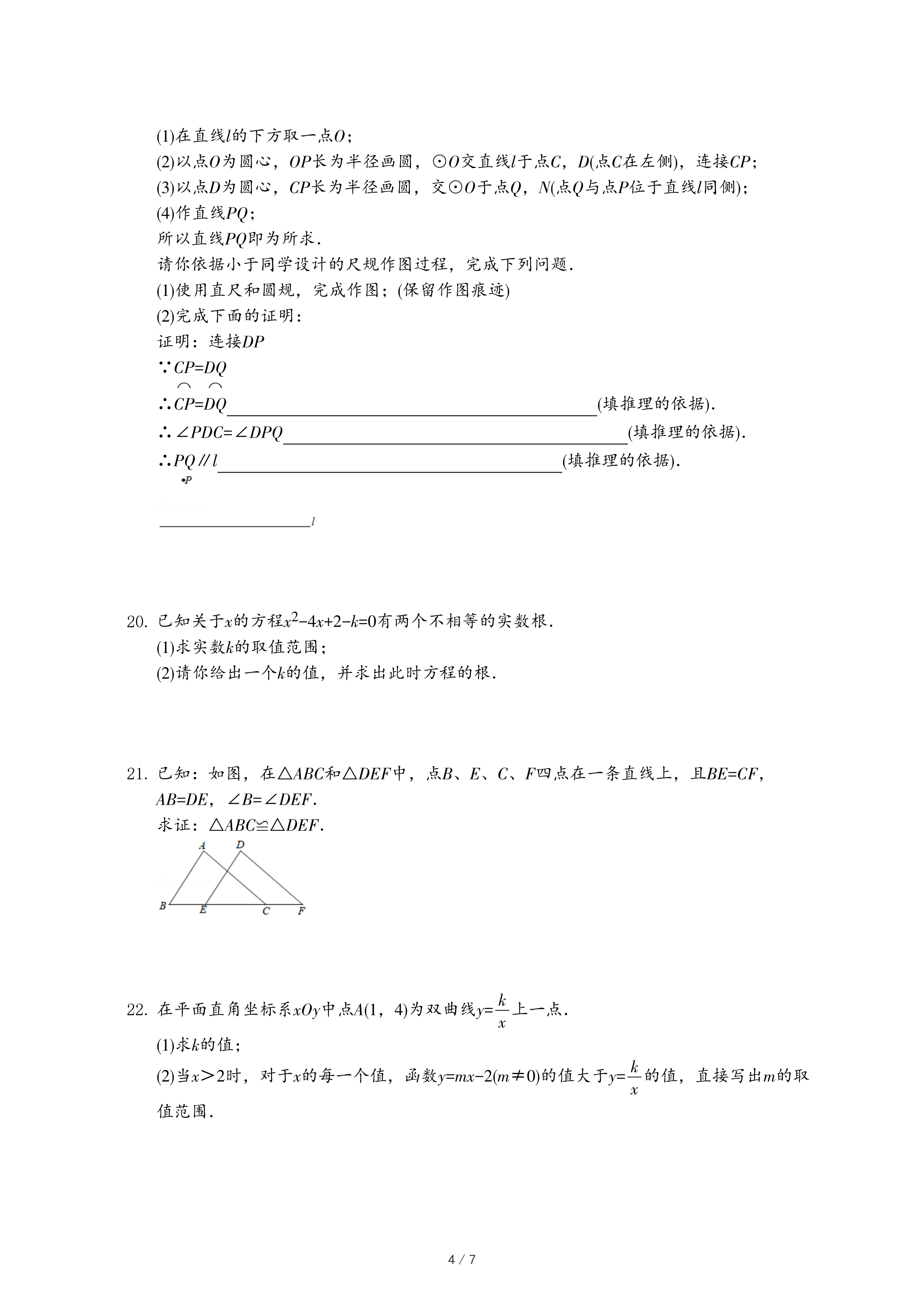
a.反映2020年中央财政脱贫专项资金分配额度的频数分布直方图如图1(数据分成8组:0<x<20,20≤x<40,40≤x<60,60≤x<80,80≤x<100,100≤x<120,120≤x<140,140≤x<160);
b.2020年中央财政脱贫专项资金在20≤x<40这一组分配的额度是(亿元):
25 28 28 30 37 37 38 39 39
(1)2020年中央财政脱贫专项资金对各省、直辖市、自治区分配额度的中位数为
(亿元);
(2)2020年中央财政脱贫专项资金对某省的分配额度为95亿元,该额度在28个省、直辖市、自治区中由高到低排第
名;
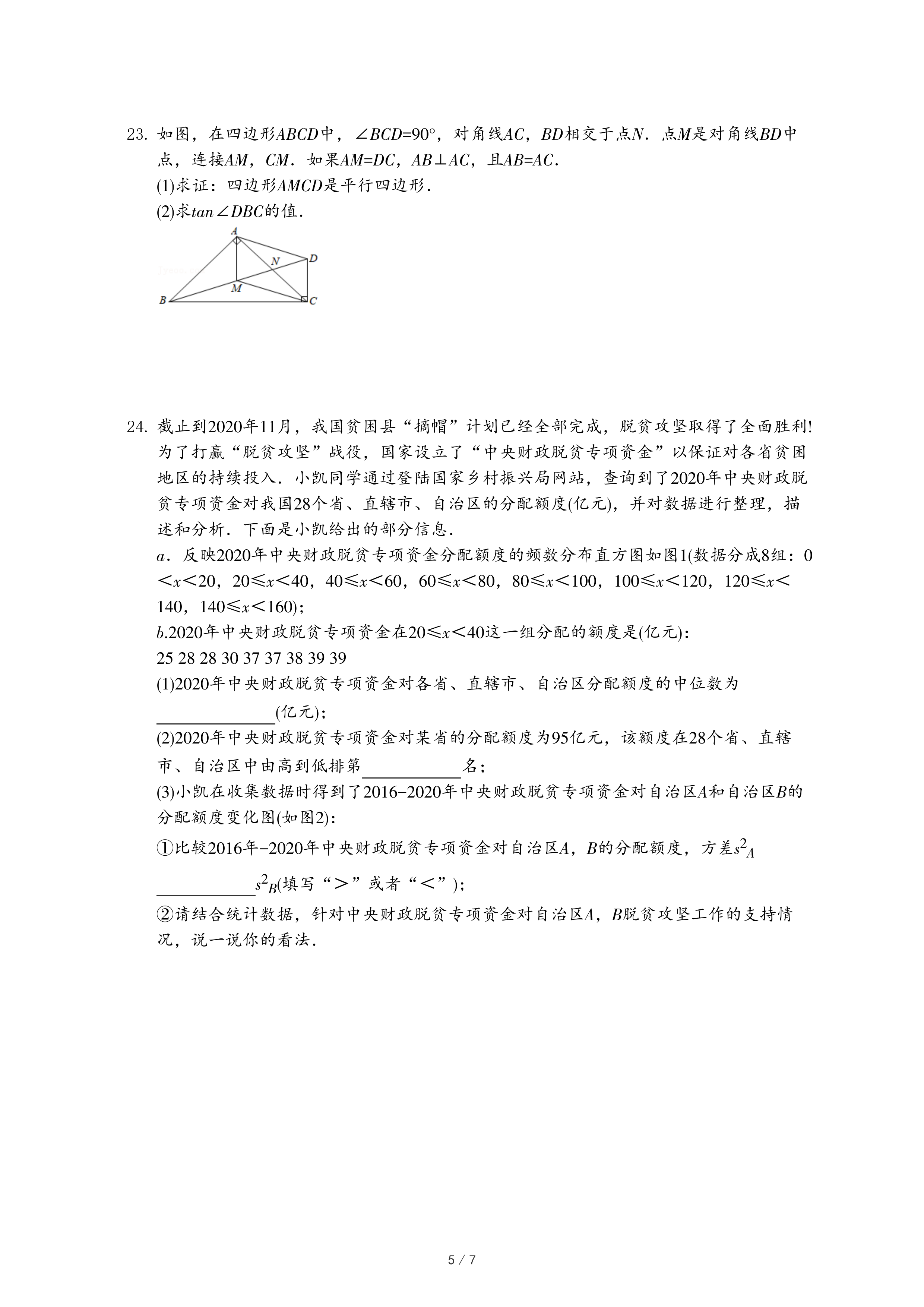
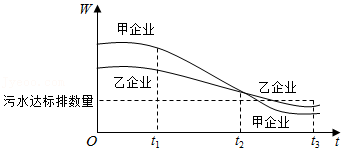
(3)小凯在收集数据时得到了2016-2020年中央财政脱贫专项资金对自治区A和自治区B的分配额度变化图(如图2):
①比较2016年-2020年中央财政脱贫专项资金对自治区A,B的分配额度,方差s
2A s
2B(填写“>”或者“<”);
②请结合统计数据,针对中央财政脱贫专项资金对自治区A,B脱贫攻坚工作的支持情况,说一说你的看法.