| 1 |
| 5 |
| 1 |
| 5 |
| 甲 | 乙 | 丙 | 丁 | |
| x | 24 | 24 | 23 | 20 |
| S2 | 1.9 | 2.1 | 2 | 1.9 |
√5 -1 |
| 2 |
| 摸到红球的次数 | 摸到白球的次数 | |
| 一组 | 13 | 7 |
| 二组 | 14 | 6 |
| 三组 | 15 | 5 |
√2 |
| 2 |
| 1 |
| 2 |
| x-1 |
| 3 |
| x-2 |
| 2 |

| 1 |
| 2 |
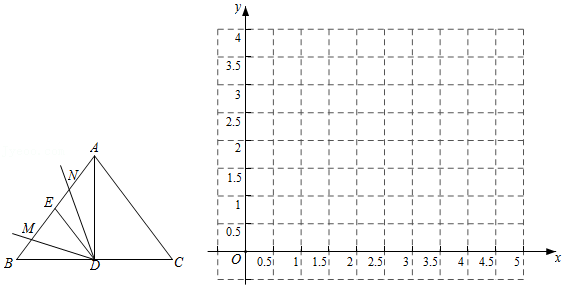
| x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
| y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
| m |
| x |
| m |
| x |