首页 > 初中试卷 > 九年级试卷 > 九年级数学试卷 > 2019年九年级数学试卷 > 2019年北京九年级数学试卷 > 2019年北京数学中考模拟试卷

【2019年北京市昌平区中考数学二模试卷】-第8页

试卷格式：2019年北京市昌平区中考数学二模试卷.PDF
试卷热词：最新试卷、2019年、北京试卷、数学试卷、九年级试卷、中考模拟试卷、初中试卷
如何查看答案以及解析
下载试卷后，用微信扫一扫扫描试卷右上角二维码即可查看【2019年北京市昌平区中考数学二模试卷】解析和视频讲解。
试卷题目
1．下列几何体中，俯视图是矩形的是(　　)
  • A.
  • B.
  • C.
  • D.
2．2019年全国两会期间其中某一天产生的信息有122863条，热度最高的三个关键词分别是：“健康”“医疗”和“教育”，请将122863用科学记数法表示(　　)
  • A. 1.22863×105
  • B. 12.2863×104
  • C. 0.122863×106
  • D. 122.863×10
3．实数a，b，c，d在数轴上对应的点的位置如图所示，则正确的结论是（　　）

  • A. |a|＞3
  • B. c﹣b＞0
  • C. a+c＞0
  • D. bd＞0
4．二元一次方程组的解是(　　)
  • A.
  • B.
  • C.
  • D.
5．如图，昌平十三陵中的部分皇陵在地图上的位置，若庆陵的位置坐标(-1，4)，长陵的位置坐标(2，0)，则定陵的位置坐标为(　　)

  • A. (5，2)
  • B. (-5，2)
  • C. (2，5)
  • D. (-5，-2)
6．如果m+n=2，那么代数式(m+
m2+n2
2n
)⋅
n
m+n
的值是(　　)
  • A. 2
  • B. 1
  • C.
    1
    2
  • D. -1
7．数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等(如图所示)”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证，下列说法不一定成立的是(　　)

  • A. S△ABC=S△ADC
  • B. S矩形NFGD=S矩形EFMB
  • C. S△ANF=S矩形NFGD
  • D. S△AEF=S△ANF
8．小明和小华是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校．如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图．则下列说法中正确的是(　　)
①小明家和学校距离1200米；
②小华乘坐公共汽车的速度是240米/分；
③小华乘坐公共汽车后7：50与小明相遇；
④小华的出发时间不变，当小华由乘公共汽车变为跑步，且跑步的速度是100米/分时，他们可以同时到达学校．

  • A. ①③④
  • B. ①②③
  • C. ①②④
  • D. ①②③④
9．如图所示的网格是正方形网格，则∠AOB      ∠COD．(填“＞”，“=”或“＜”)

10．代数式
√x-1
在实数范围内有意义，则x的取值范围是      ．
11．若正多边形的一个内角等于120°，则这个正多边形的边数是       ．
12．在一个不透明的盒子里装有红、黑两种颜色的球共60只，这些球除颜色外其余完全相同．为了估计红球和黑球的个数，七(2)班的数学学习小组做了摸球试验．他们将球搅匀后，从盒子里随机摸出一个球记下颜色，再把球放回盒子中，多次重复上述过程，得到表中的一组统计数据：
摸球的次数n 50 100 300 500 800 1000 
摸到红球的次数m 14 33 95 155 241 298 
摸到红球的频率
m
n
 		0.28 0.33 0.317 0.31 0.301 0.298 

请估计：当次数n足够大时，摸到红球的频率将会接近       ．(精确到0.1)
13．某学校决定用1200元购买篮球和排球，其中篮球每个120元，排球每个90元，至少买一个排球，在购买资金恰好用尽的情况下，购买方案有      种．
14．如图，在平行四边形ABCD中，E是边AB的中点，连接DE交对角线AC于点F，若CF=6，则AF的长为      ．

15．今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人的得票数内．全村设有四个投票点，目前第一、第二、第三投票点已公布投票结果，剩下第四投票点尚未公布投票结果，如表所示：(单位：票)
投票点 候选人 废票 合计 
甲 乙 丙 
一 200 211 147 12 570 
二 286 85 244 15 630 
三 97 41 205 7 350 
四         250 

三名候选人      有机会当选村长(填甲、乙、丙)，并写出你的推断理由      
      
      
      
      
      
      
      
      
      ．
16．“五一黄金周”期间李师傅一家开车去旅游，出发前查看了油箱里有50升油，下面的两幅图分别描述了行驶里程及耗油情况，行驶130公里时，油箱里剩油量为      升．

17．计算：
√8
+(-2019)0-4sin45°+|-2|．
18．解不等式组：
19．在数学课上，老师提出如下问题：如何使用尺规完成“过直线l外一点P作已知直线l的平行线”．
小明的作法如下：
①在直线l上取一点A，以点A为圆心，AP长为半径作弧，交直线l于点B；
②分别以P，B为圆心，以AP长为半径作弧，两弧相交于点Q(与点A不重合)；
③作直线PQ．
所以直线PQ就是所求作的直线．
根据小明的作图过程，
(1)使用直尺和圆规，补全图形；(保留作图痕迹)
(2)完成下面的证明．
证明：∵AB=AP=      =      ．
∴四边形ABQP是菱形(      )(填推理的依据)．
∴PQ∥l．

20．已知：关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根．
(1)求m的取值范围；
(2)写出一个满足条件的m的值，并求此时方程的根．
21．如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF=BE，连接DF．
(1)求证：四边形AEFD是矩形；
(2)若BF=8，DF=4，求CD的长．

22．如图，在平面直角坐标系xOy中，函数y=
k
x
(x＞0)的图象与直线y=2x-2交于点为A(2，m)．
(1)求k，m的值；
(2)点B为函数y=
k
x
(x＞0)的图象上的一点，直线AB与y轴交于点C，当AC=2AB时，求点C的坐标．

23．如图，在Rt△ABC中，∠C=90°，以AC为直径的⊙O交AB于点D，点Q为CA延长线上一点，延长QD交BC于点P，连接OD，∠ADQ=
1
2
∠DOQ．
(1)求证：PD是⊙O的切线；
(2)若AQ=AC，AD=2时，求BP的长．

24．近日，某中学举办了一次以“赏中华诗词、寻文化基因、品生活之美”为主题的诗词大会比赛，初一和初二两个年级各有600名学生参加．为了更好地了解本次比赛成绩的分布情况，学校分别从两个年级随机抽取了若干名学生的成绩作为样本进行分析．下面是初二年级学生成绩样本的频数分布表和频数分布直方图(不完整，每组分数段中的分数包括最低分，不包括最高分)：
初二学生样本成绩频数分布表
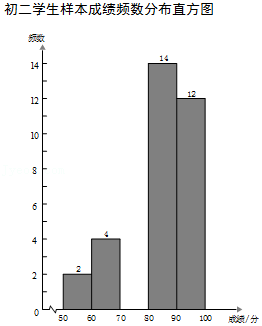
分组/分 频数 频率 
50～60 2        
60～70 4 0.10 
70～80        0.20 
80～90 14 0.35 
90～100 12 0.30 
合计 40 1.00 

请根据所给信息，解答下列问题：
(1)补全成绩频数分布表和频数分布直方图；
(2)若初二学生成绩样本中80～90分段的具体成绩为：80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
①根据上述信息，估计初二学生成绩的中位数为      ；
②若初一学生样本成绩的中位数为80，甲同学在比赛中得到了82分，在他所在的年级中位居275名，根据上述信息推断甲同学所在年级为      (填“初一”或“初二”)；
③若成绩在85分及以上为“优秀”，请你根据抽取的样本数据，估计初二年级学生中达到“优秀”的学生人数为      人．

25．如图，在△ABC中，∠C=90°，AC=BC，AB=6cm，E是线段AB上一动点，D是BC的中点，过点C作射线CG，使CG∥AB，连接ED，并延长ED交CG于点F，连接AF．设A，E两点间的距离为xcm，A，F两点间的距离为y1cm，E，F两点间的距离为y2cm．
小丽根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．
下面是小丽的探究过程，请补充完整：
(1)按照表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；
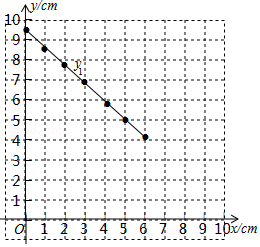
x/cm 0 1 2 3 4 5 6 
y1/cm 9.49 8.54 7.62 6.71 5.83 5.00 4.24 
y2/cm 9.49 7.62 5.83   3.16 3.16 4.24 

(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x，y1)，(x，y2)，并画出函数y1，y2的图象；

(3)结合函数图象，解决问题：当△AEF为等腰三角形时，AE的长度约为      cm．

26．在平面直角坐标系xOy中，直线y=x+1与抛物线y=ax2+bx+3a交于点A和点B，点A在x轴上．
(1)点A的坐标为      ．
(2)①用等式表示a与b之间的数量关系，并求抛物线的对称轴；
②当3
√2
≤AB≤5
√2
时，结合函数图象，求a的取值范围．
27．在正方形ABCD中，AC是一条对角线，点E是边BC上的一点(不与点C重合)，连接AE，将△ABE沿BC方向平移，使点B与点C重合，得到△DCF，过点E作EG⊥AC于点G，连接DG，FG．
(1)如图1，①依题意补全图1；
②判断线段FG与DG之间的数量关系与位置关系，并证明；
(2)已知正方形的边长为6，当∠AGD=60°时，求BE的长．

28．对于平面直角坐标系xOy中的图形M及以点C为圆心，1为半径的⊙C，给出如下定义：P为图形M上任意一点，Q为⊙C上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M到⊙C的“圆距离”，记作d(M-C)．
(1)点C在原点O时，
①记点A(4，3)为图形M，则d(M-O)=      ；
②点B与点A关于x轴对称，记线段AB为图形M，则d(M-O)=      ；
③记函数y=kx+4(k＞0)的图象为图形M，且d(M-O)≤1，直接写出k的取值范围；
(2)点C坐标为(t，0)时，点A，B与(1)中相同，记∠AOB为图形M，且d(M-C)=1，直接写出t的值．
查看全部题目
【2019年北京市昌平区中考数学二模试卷】标签
中考模拟试卷 最新试卷 北京试卷 2019年试卷 初中试卷 九年级试卷 数学试卷
1 2 3 4 5 6 7 8 9
下载高清试卷