2021年北京市怀柔区中考数学一模试卷-乐乐课堂

1．如图是某几何体的三视图，该几何体是(　　)

A. 圆柱
B. 球
C. 三棱柱
D. 长方体

2．2021年2月24日6时29分，我国自主研制的首个火星探测器“天问一号”成功实施第三次近火制动，进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道．将59000用科学记数法表示应为(　　)

A. 0.59×10⁵
B. 5.9×10⁵
C. 5.9×10⁴
D. 5.9×10³

3．七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形中，是轴对称图形的是(　　)

A.
B.
C.
D.

4．如图是一个可以自由转动的转盘，转盘分成4个大小相同的扇形，颜色分为灰、白二种颜色，指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时，当作指向右边的扇形)，则指针指向白色区域的概率是(　　)

A.
1
4
B.
1
2
C.
3
4
D. 1

5．已知正多边形的一个外角等于60°，则该正多边形的边数为(　　)

A. 3
B. 4
C. 5
D. 6

6．实数a与b在数轴上对应点的位置如图所示，则正确的结论是(　　)

A. a＜0
B. a＜b
C. b+5＞0
D. |a|＞|b|

7．已知x=1是不等式2x-b＜0的解，b的值可以是(　　)

A. 4
B. 2
C. 0
D. -2

8．如图，AB是⊙O直径，点C，D将⌒AB分成相等的三段弧，点P在⌒AC上．已知点Q在⌒AB上且∠APQ=115°，则点Q所在的弧是(　　)

A. ⌒AP
B. ⌒PC
C. ⌒CD
D. ⌒DB

9．若式子

√x-1

有意义，则实数x的取值范围是．

10．方程组的解为．

11．如图，在一束平行光线中插入一张对边平行的纸板．如果图中∠1是70°，那么∠2的度数是．

12．若

√2

+a的值为有理数，请你写出一个符合条件的实数a的值．

13．计算：(

x²

x-1

-

1

x-1

)•

1

x+1

= ．

14．已知关于x的方程x²-(m+2)x+4=0有两个相等的实数根，则m的值是．

15．图1中的直角三角形有一条直角边长为3，将四个图1中的直角三角形分别拼成如图2，图3所示的正方形，其中阴影部分的面积分别记为S₁，S₂，则S₁-S₂的值为．

16．图1是一个2×2正方形网格，两条网格线的交点叫做格点，甲、乙两人在网格中进行游戏，规则如下：
游戏规则
a．两人依次在网格中画线段，线段的起点和终点均为格点；
b．新画线段的起点为前一条线段的终点，且与任意已画出线段不能有其他公共点；
c．已画出线段的所有端点中，任意三个端点不能在同一条直线上；
d．当某人无法画出新的线段时，则另一人获胜．
如图2，甲先画出线段AB，乙随后画出线段BC．若这局游戏继续进行下去，最终的获胜者是 (填“甲”，“乙”或“不确定”)．

17．计算：|-

√2

|-2cos45°+(π-1)⁰+

√12

．

18．解不等式组：．

19．如图，点B，E，C，F在一条直线上，AB∥DE，AB=DE，BE=CF．求证：∠A=∠D．

20．已知a²+a-1=0，求代数式(a+2)(a-2)+a(a+2)的值．

21．如图，矩形ABCD中，点E在BC上，AE⊥ED．
(1)求证：△ABE∽△ECD；
(2)F为AE延长线上一点，满足EF=AE，连接DF交BC于点G．若AB=2，BE=1，求GC的长．

22．我国是世界上最早发明历法的国家之一．《周礼》中记载：垒土为圭，立木为表，测日影，正地中，定四时．如图1，圭是地面上一根水平标尺，指向正北，表是一根垂直于地面的杆．正午，表的日影(即表影)落在圭上，根据表影的长度可以测定节气．
在一次数学活动课上，要制作一个圭表模型．如图2，地面上放置一根长2m的杆AB，向正北方向画一条射线BC，在BC上取点D，测得BD=1.5m，AD=2.5m．
(1)判断：这个模型中AB与BC是否垂直．答： (填“是”或“否”)；你的理由是：．
(2)某地部分节气正午时分太阳光线与地面夹角α的值，如下表：

节气	夏至	秋分	冬至
太阳光线与地面夹角α	74°	50°	27°

①记夏至和冬至时表影分别为BM和BN，利用上表数据，在射线BC上标出点M和点N的位置；
②记秋分时的表影为BP，推测点P位于．
A.线段MN中点左侧
B.线段MN中点处
C.线段MN中点右侧

23．已知直线l：y=kx(k≠0)经过点A(-1，2)．点P为直线l上一点，其横坐标为m．过点P作y轴的垂线，与函数y=

4

x

(x＞0)的图象交于点Q．
(1)求k的值；
(2)①求点Q的坐标(用含m的式子表示)；
②若△POQ的面积大于3，直接写出点P的横坐标m的取值范围．

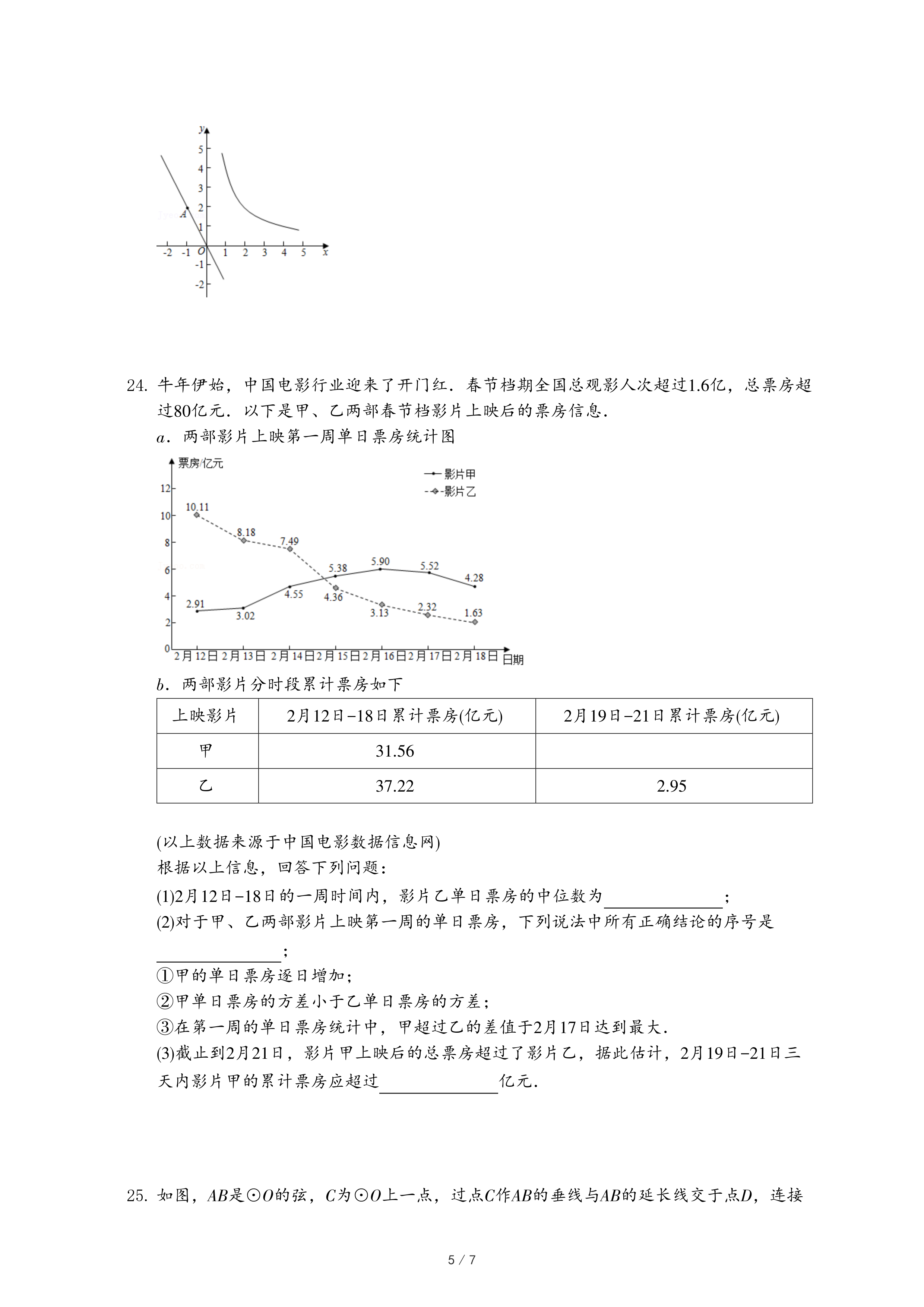
24．牛年伊始，中国电影行业迎来了开门红．春节档期全国总观影人次超过1.6亿，总票房超过80亿元．以下是甲、乙两部春节档影片上映后的票房信息．
a．两部影片上映第一周单日票房统计图

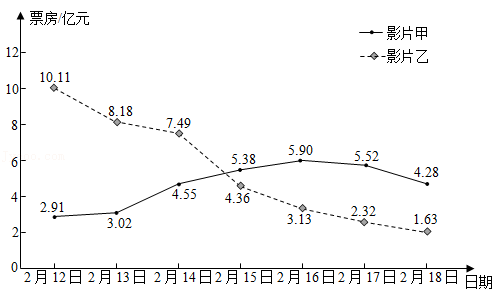
b．两部影片分时段累计票房如下

上映影片	2月12日-18日累计票房(亿元)	2月19日-21日累计票房(亿元)
甲	31.56
乙	37.22	2.95

(以上数据来源于中国电影数据信息网)
根据以上信息，回答下列问题：
(1)2月12日-18日的一周时间内，影片乙单日票房的中位数为      ；
(2)对于甲、乙两部影片上映第一周的单日票房，下列说法中所有正确结论的序号是      ；
①甲的单日票房逐日增加；
②甲单日票房的方差小于乙单日票房的方差；
③在第一周的单日票房统计中，甲超过乙的差值于2月17日达到最大．
(3)截止到2月21日，影片甲上映后的总票房超过了影片乙，据此估计，2月19日-21日三天内影片甲的累计票房应超过      亿元．

25．如图，AB是⊙O的弦，C为⊙O上一点，过点C作AB的垂线与AB的延长线交于点D，连接BO并延长，与⊙O交于点E，连接EC，∠ABE=2∠E．
(1)求证：CD是⊙O的切线；
(2)若tanE=

1

3

，BD=1，求AB的长．

26．在平面直角坐标系xOy中，已知抛物线y=ax²-2ax+a-2(a＞0)．分别过点M(t，0)和点N(t+2，0)作x轴的垂线，交抛物线于点A和点B．记抛物线在A，B之间的部分为图象G(包括A，B两点)．
(1)求抛物线的顶点坐标；
(2)记图象G上任意一点的纵坐标的最大值与最小值的差为m．
①当a=2时，若图象G为轴对称图形，求m的值；
②若存在实数t，使得m=2，直接写出a的取值范围．

27．如图，在△ABC中，AB=AC，∠BAC=40°，作射线CM，∠ACM=80°．D在射线CM上，连接AD，E是AD的中点，C关于点E的对称点为F，连接DF．
(1)依题意补全图形；
(2)判断AB与DF的数量关系并证明；
(3)平面内一点G，使得DG=DC，FG=FB，求∠CDG的值．

28．在平面直角坐标系xOy中，对于点A和线段MN，如果点A，O，M，N按逆时针方向排列构成菱形AOMN，且∠AOM=α，则称线段MN是点A的“α-相关线段”．例如，图1中线段MN是点A的“30°-相关线段”．
(1)已知点A的坐标是(0，2)．
①在图2中画出点A的“30°-相关线段”MN，并直接写出点M和点N的坐标；
②若点A的“α-相关线段”经过点(

√3

，1)，求α的值；
(2)若存在α，β(α≠β)使得点P的“α-相关线段”和“β-相关线段”都经过点(0，4)，记PO=t，直接写出t的取值范围．

【2021年北京市怀柔区中考数学一模试卷】-第5页