17．计算：-3tan30°+(2019-π)⁰-()^-1．

18．解方程：+=3．

19．如图，E为AB中点，CE⊥AB于点E，AD=5，CD=4，BC=3，求证：∠ACD=90°．

20．研究发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的．讲课开始时，学生的注意力激增，中间有一段时间，学生的注意力保持平稳状态，随后开始分散．学生注意力指标数y随时间x变化的函数图象如图所示(y越大表示学生注意力越集中)．当0≤x≤10时，图象是抛物线的一部分；当10≤x≤20和20≤x≤45时，图象是线段．根据图象回答问题：
(1)课堂上，学生注意力保持平稳状态的时间段是      ．
(2)结合函数图象回答，一道几何综合题如果需要讲25分钟，老师最好在上课后大约第      分钟到第      分钟讲这道题，能使学生处于注意力比较集中的听课状态．

21．如图，在四边形ABCD中，AD∥BC，AE平分∠BAD，交BC于点E，作EF∥AB，交AD于点F，AE与BF交于点P，连接CF，CF=EF．
(1)求证：四边形ABEF是菱形；
(2)若BF=4，tan∠FBC=，求EC的长．

22．如图，在平面直角坐标系xOy中，直线y=-x+1与函数y=的图象交于A(-2，a)，B两点．
(1)求a，k的值；
(2)已知点P(0，m)，过点P作平行于x轴的直线l，交函数y=的图象于点C(x₁，y₁)，交直线y=-x+1的图象于点D(x₂，y₂)，若|x₁|＞|x₂|，结合函数图象，直接写出m的取值范围．

23．如图，AB是⊙O的直径，弦EF⊥AB于点C，点D是AB延长线上一点，∠A=30°，∠D=30°．
(1)求证：FD是⊙O的切线；
(2)取BE的中点M，连接MF，若MF=，求⊙O的半径．

24．2019年4月23日世界读书日这天，某校初三年级的小记者，就2018年寒假读课外书数量(单位：本)做了调查，他们随机调查了甲、乙两个班的10名同学，调查过程如下，请补充完整．
收集数据甲、乙两班被调查者读课外书数量(单位：本)统计如下：
甲：1，9，7，4，2，3，3，2，7，2
乙：2，6，6，3，1，6，5，2，5，4
整理、描述数据绘制统计表如下，请补全下表：

分析数据、推断结论
(1)该校初三乙班共有40名同学，你估计2018年寒假读6本书的同学大概有      人；
(2)你认为甲、乙两班同学寒假读书情况更好的是，理由是：      ．

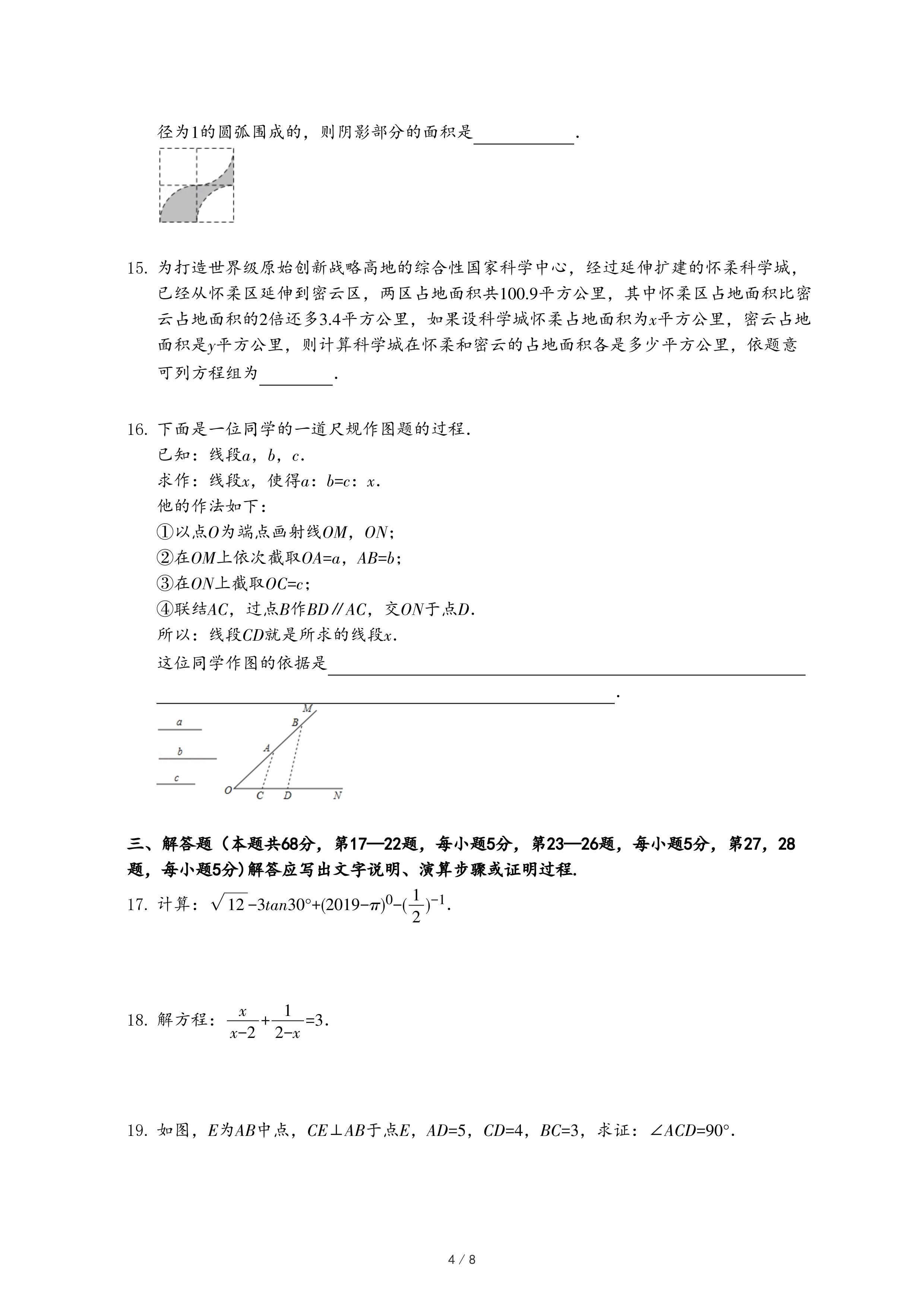
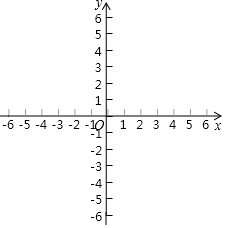25．阅读材料：
1903年，英国物理学家卢瑟福通过实验证实，放射性物质放出射线后，这种物质的质量将减少，物质所剩的质量与时间成某种函数关系．镭的质量由m₀缩减到m₀需1620年，由m₀缩减到m₀需1620年，由m₀缩减到m₀需1620年，即镭的质量缩减为原来的一半所用的时间是一个不变的量--1620年，一般把1620年称为镭的半衰期．
实际上，所有放射性物质都有自己的半衰期．铀的半衰期为4.5×10⁹年，蜕变后的铀最后成为铅．科学家们测出一块岩石中现在含铀和铅的质量，便可以利用半衰期算出从原来含铀量到现在含铀量经过了多少时间，从而推算出这块岩石的年龄．
根据以上材料回答问题：
(1)设开始时岩石中含有铀的质量为m₀千克，经过n个半衰期后，剩余的铀的质量为m₁千克，下表是m₁随n的变化情况，请补充完整：

(2)写出矿石中剩余的铀的质量m₁与半衰期n之间的函数关系；
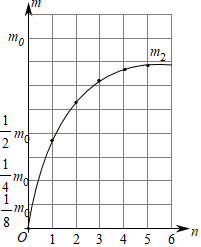
(3)设铀衰变后完全变成铅，如图是岩石中铅的质量m₂与半衰期n的函数关系图象，请在同一坐标系中，利用描点法画出岩石中含铀的质量m₁与半衰期n的函数关系图象：
(4)结合函数图象，估计经过      个半衰期(精确到0.1)，岩石中铀铅质量相等．

26．在平面直角坐标系xOy中，直线y=x与抛物线y=ax²-(3+a)x+3(a≠0)交于A，B两点，并且OA＜OB．
(1)当a=1时，求抛物线与x轴的交点坐标；
(2)当2≤OB≤4时，求a的取值范围．

27．如图，在梯形ABCD中，AD∥BC(BC＞AD)，∠D=90°，BC=CD=12，∠ABE=45°，若AE=10．求CE的长度．

28．在平面直角坐标系xOy中，对于两个点A，B和图形ω，如果在图形ω上存在点P，Q(P，Q可以重合)，使得AP=2BQ，那么称点A与点B是图形ω的一对“倍点”．
已知⊙O的半径为1，点B(0，3)．
(1)①点B到⊙O的最大值，最小值；
②在A₁(5，0)，A₂(0，10)，A₃(，)这三个点中，与点B是⊙O的一对“倍点”的是      ；
(2)在直线y=x+b上存在点A与点B是⊙O的一对“倍点”，求b的取值范围；
(3)正方形MNST的顶点M(m，1)，N(m+1，1)，若正方形上的所有点与点B都是⊙O的一对“倍点”，直接写出m的取值范围．