



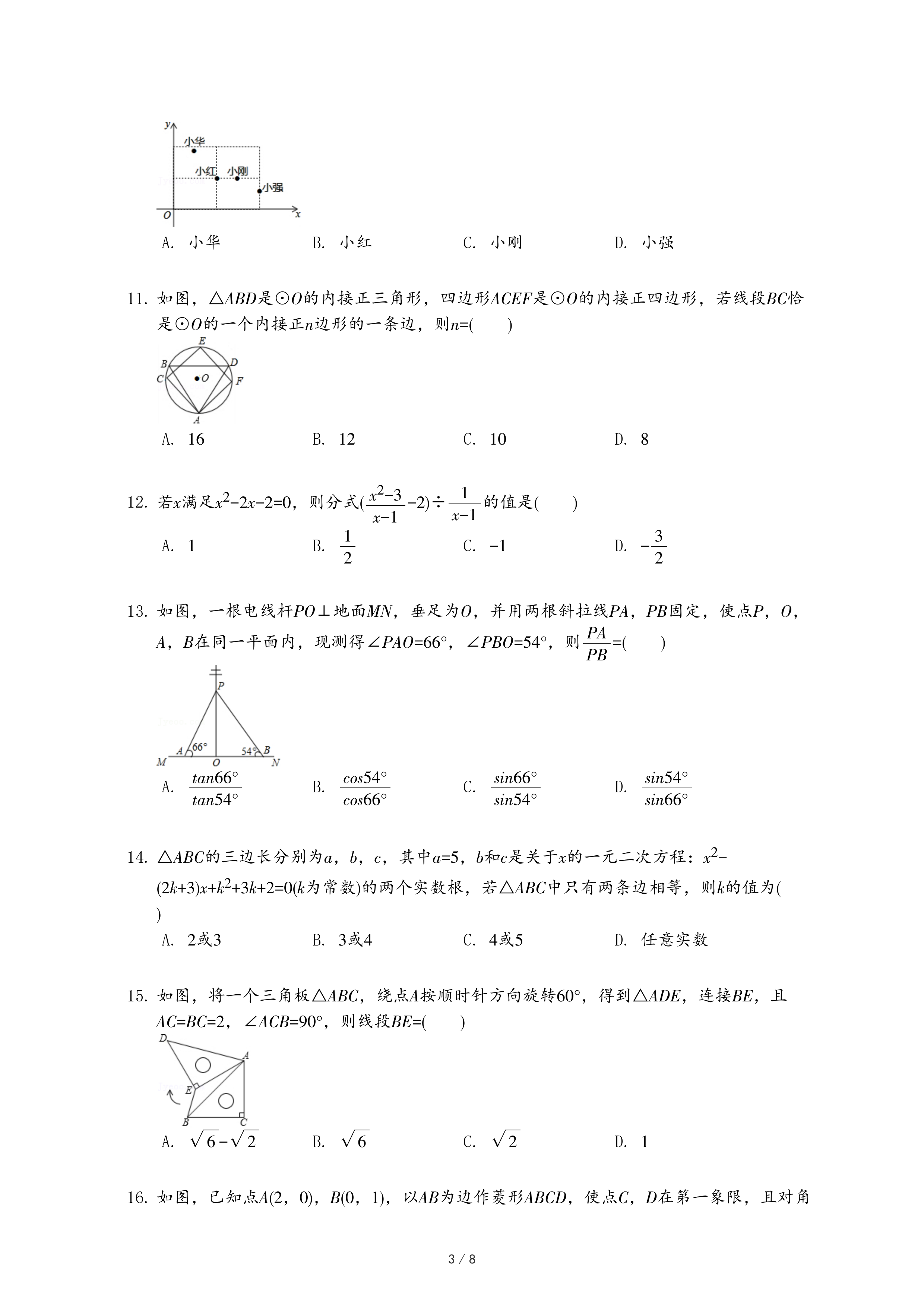










| 休闲类型 | 休闲方式 | 人数 |
| A | 老年大学 | 50 |
| B | 老年合唱队 | 350 |
| C | 老年舞蹈队 | 400 |
| D | 太极拳 | 200 |
| E | 其它方式 | 500 |
| 7 |
| 30 |
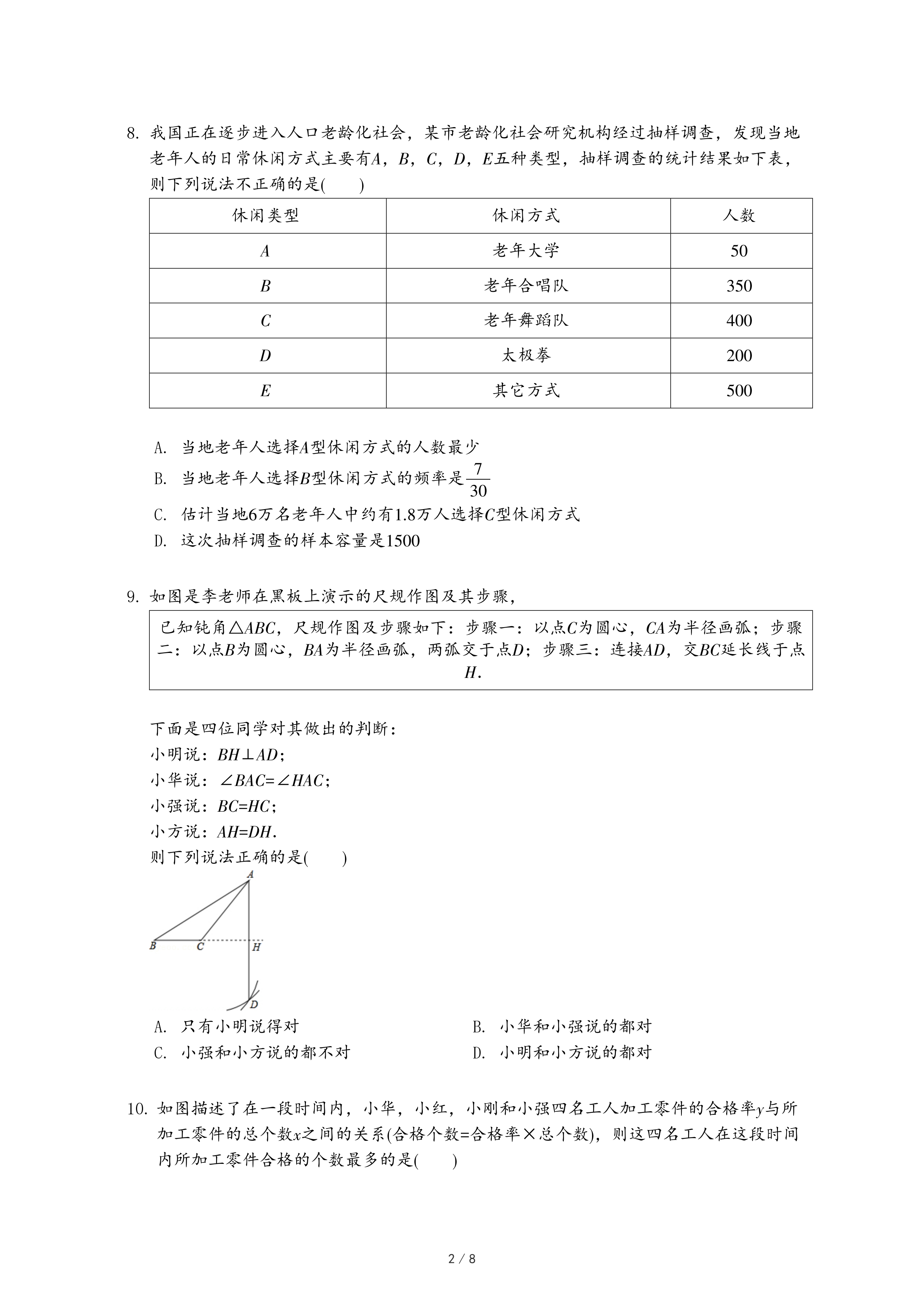
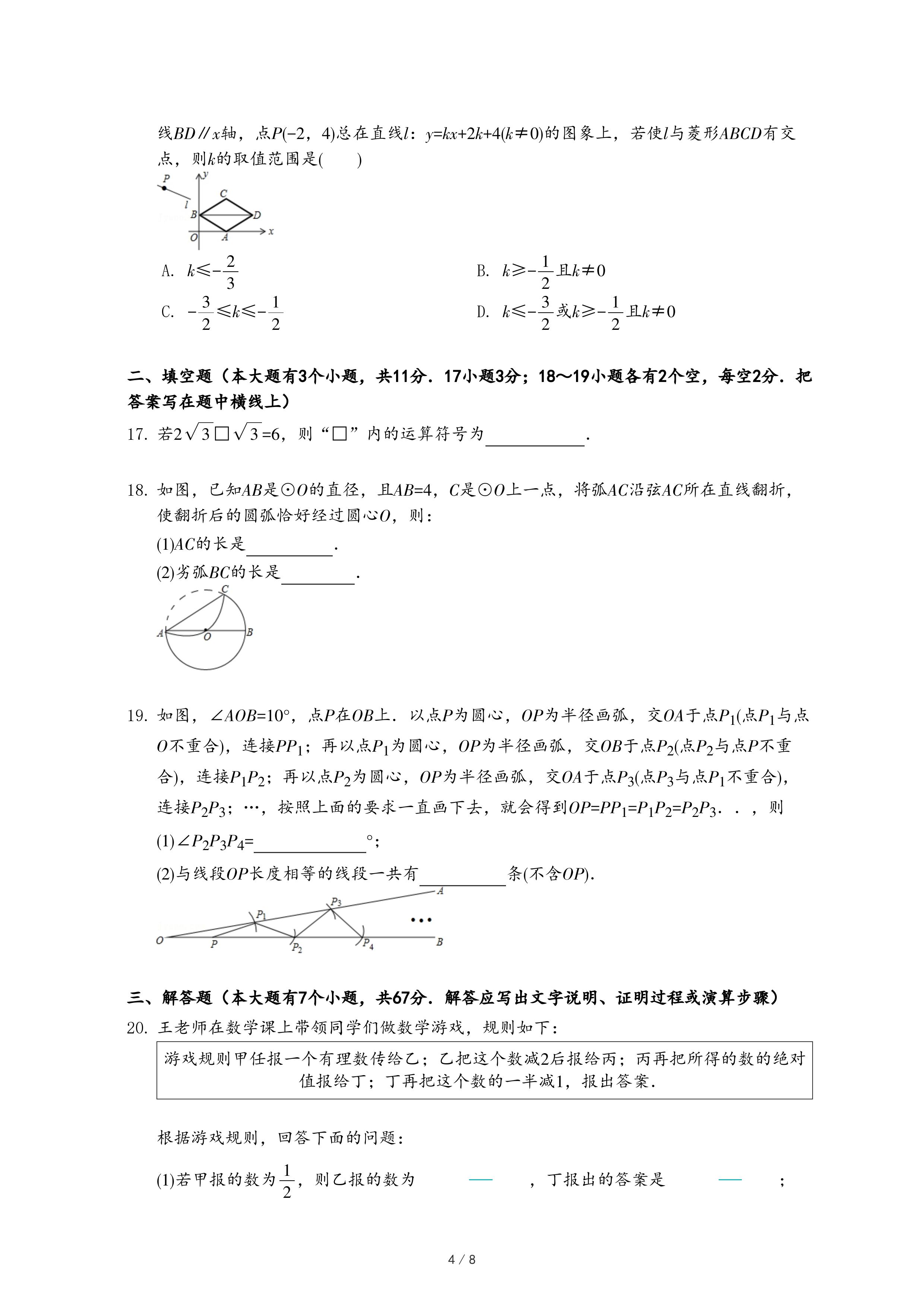
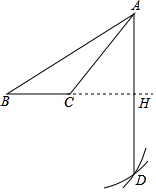
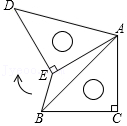
| 已知钝角△ABC,尺规作图及步骤如下:步骤一:以点C为圆心,CA为半径画弧;步骤二:以点B为圆心,BA为半径画弧,两弧交于点D;步骤三:连接AD,交BC延长线于点H. |
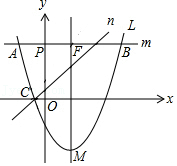
| x2-3 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| 2 |
| 3 |
| 2 |
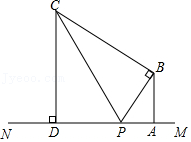
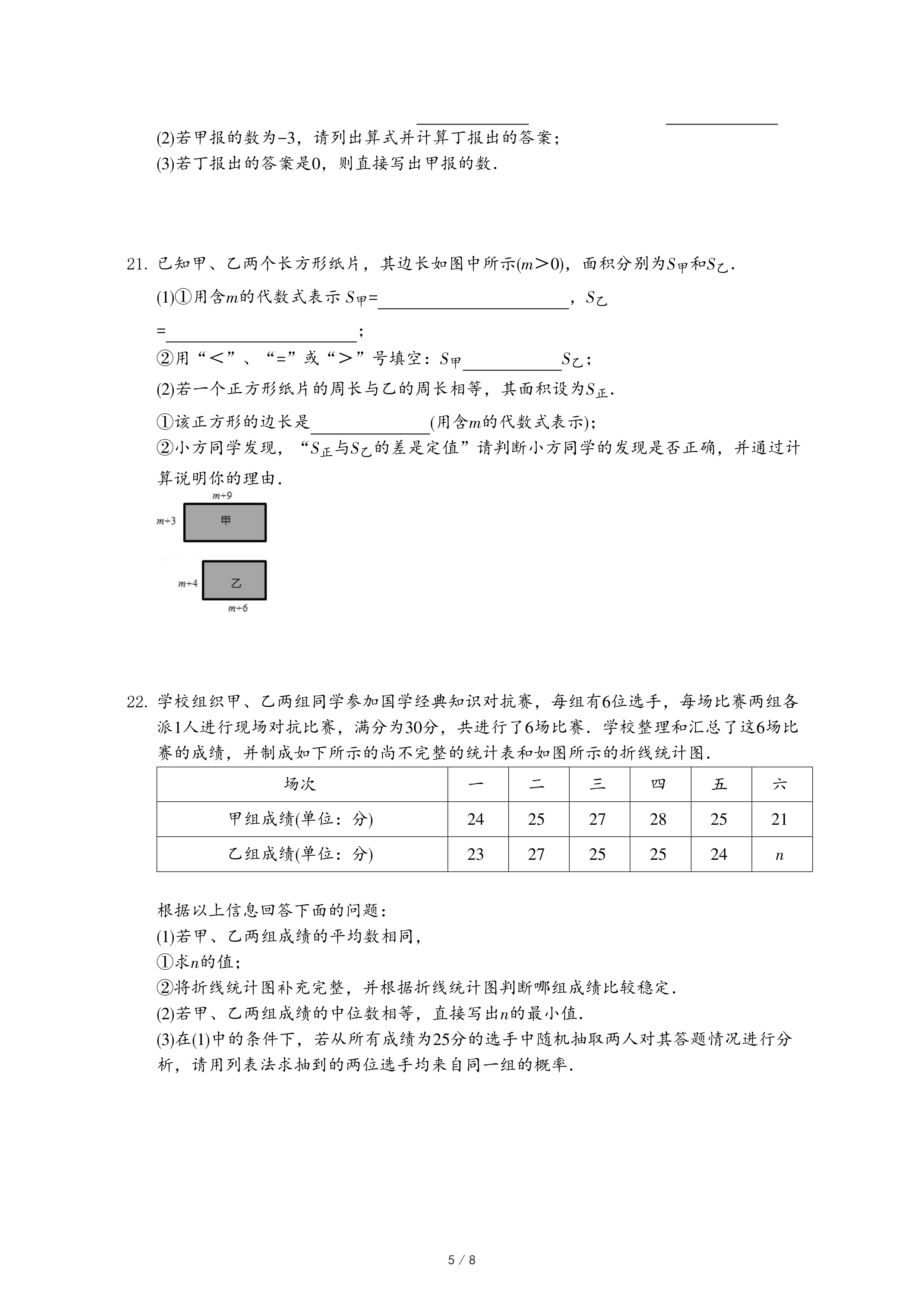
| PA |
| PB |
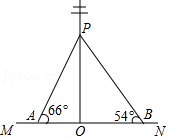
| tan66° |
| tan54° |
| cos54° |
| cos66° |
| sin66° |
| sin54° |
| sin54° |
| sin66° |
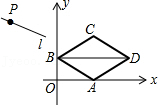
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
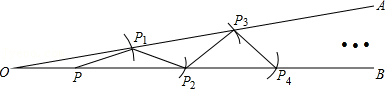
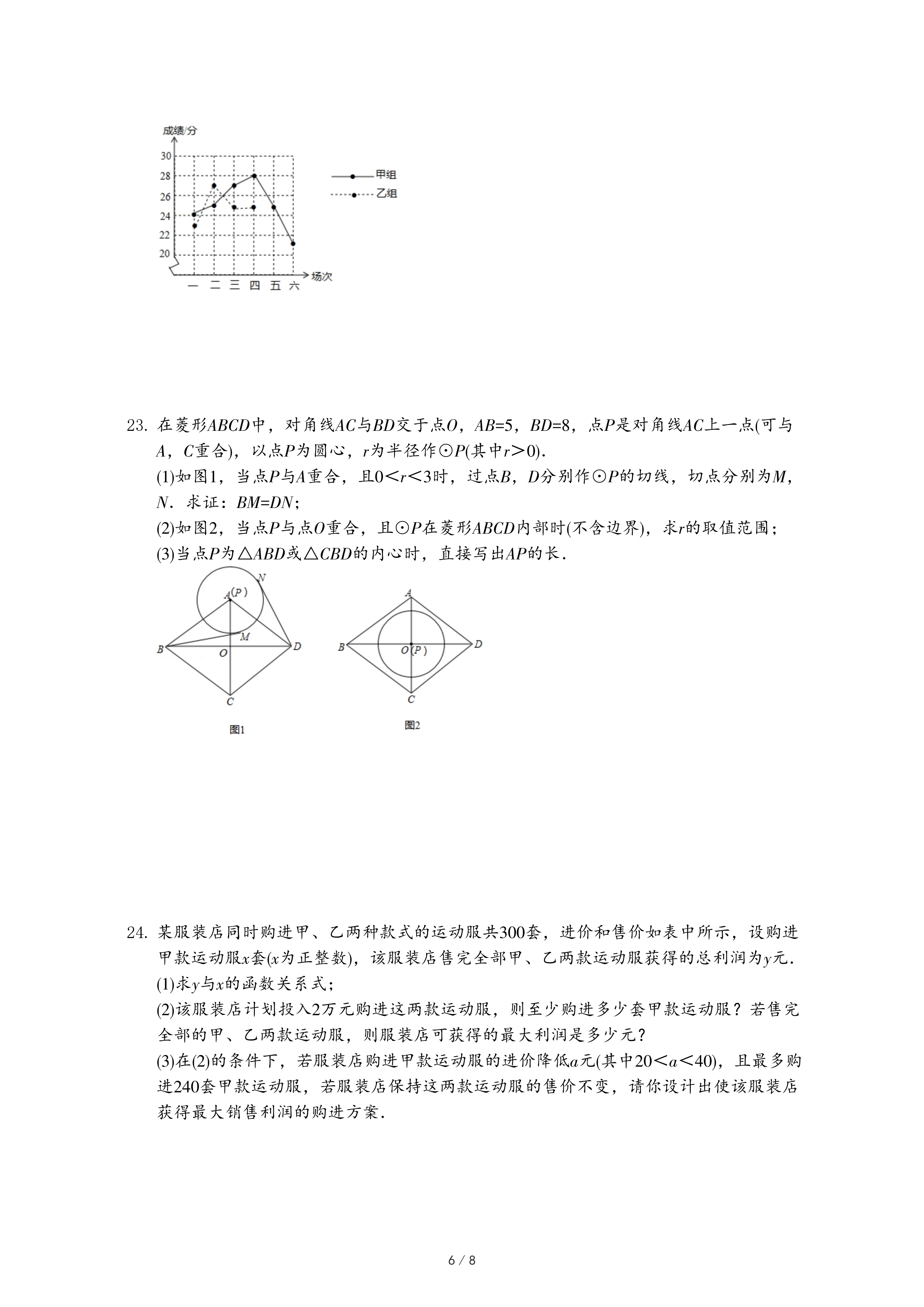
| 游戏规则甲任报一个有理数传给乙;乙把这个数减2后报给丙;丙再把所得的数的绝对值报给丁;丁再把这个数的一半减1,报出答案. |
| 1 |
| 2 |
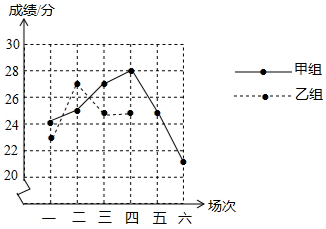
| 场次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲组成绩(单位:分) | 24 | 25 | 27 | 28 | 25 | 21 |
| 乙组成绩(单位:分) | 23 | 27 | 25 | 25 | 24 | n |
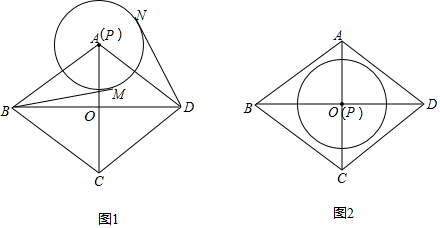
| 运动服款式 | 甲款 | 乙款 |
| 进价(元/套) | 60 | 80 |
| 售价(元/套) | 100 | 150 |