28.在平面直角坐标系xOy中,点P为一定点,点P和图形W的“旋转中点”定义如下:点Q是图形W上任意一点,将点Q绕原点顺时针旋转90°,得到点Q',点M为线段PQ'的中点,则称点M为点P关于图形W的“旋转中点”.
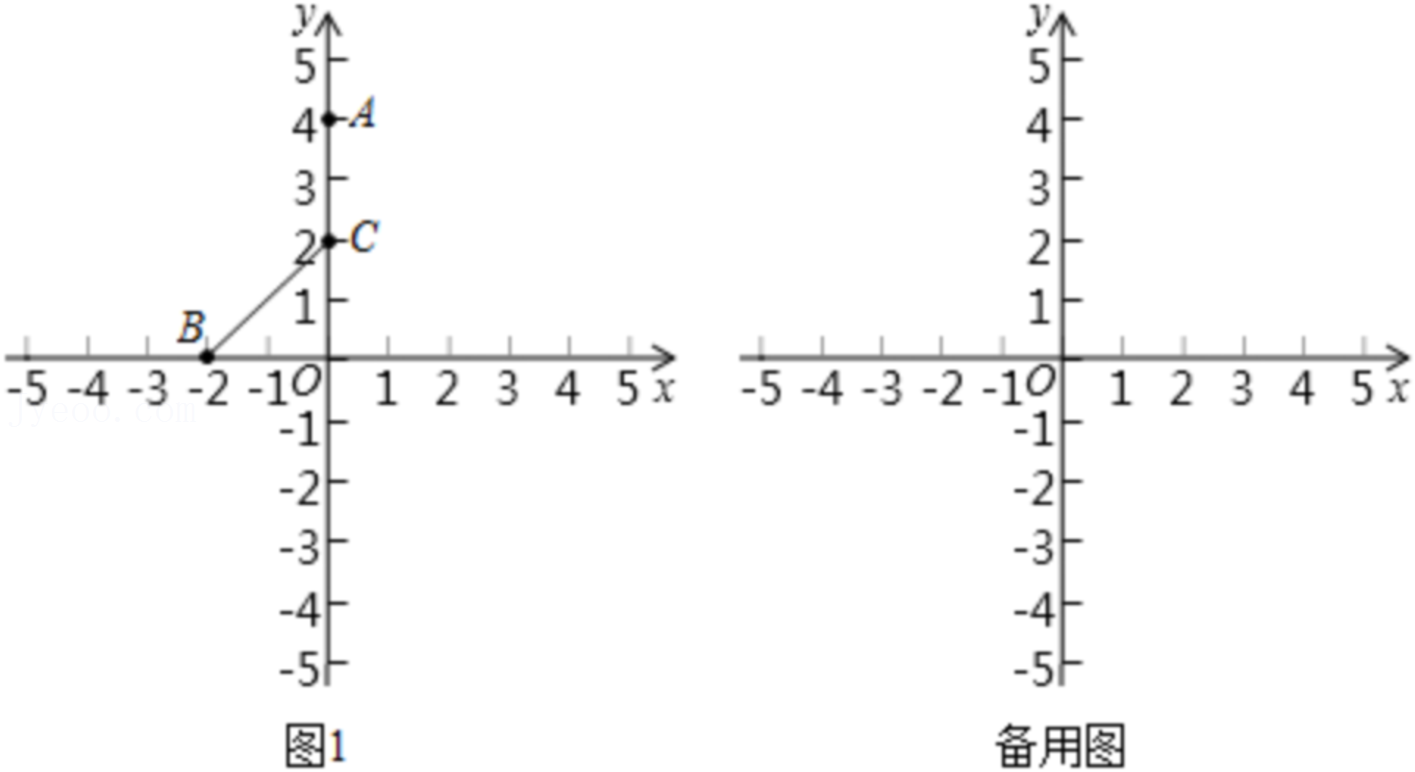
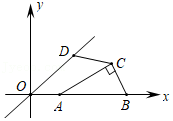
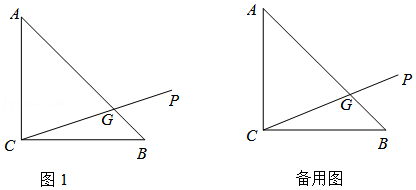
(1)如图1,已知点A(0,4),B(-2,0),C(0,2),
①在点H(0,3),G(1,1),N(2,2)中,点
是点A关于线段BC的“旋转中点”;
②求点A关于线段BC的“旋转中点”的横坐标m的取值范围;
(2)已知点D(t,0),E(t+2,0),F(3,0),⊙O的半径为2.若⊙O的内部(不包括边界)存在点F关于线段DE的“旋转中点”,求出t的取值范围.