2022年北京市东城区中考数学二模试卷-乐乐课堂

1．国家速滑馆又称“冰丝带”，是2022年北京冬季奥运会唯一新建的冰上竞赛场馆．它采用全冰面设计，冰面面积达12000平方米，将12000用科学记数法表示应为(　　)

A. 0.12×10⁵
B. 1.2×10⁴
C. 1.2×10⁵
D. 12×10³

2．如图是某一几何体的展开图，该几何体是(　　)

A. 三棱柱
B. 四棱柱
C. 圆柱
D. 圆锥

3．如图，点O在直线AB上，OC⊥OD．若∠BOD=30°，则∠AOC的大小为(　　)

A. 120°
B. 130°
C. 140°
D. 150°

4．下列图形中，既是中心对称图形又是轴对称图形的是(　　)

A.
B.
C.
D.

5．方程组的解是(　　)

A.
B.
C.
D.

6．下列运算结果正确的是(　　)

A. 3a-a=2
B. a²•a⁴=a⁸
C. (a+2)(a-2)=a²-4
D. (-a)²=-a²

7．在平面直角坐标系中，将点M(4，5)向左平移3个单位，再向上平移2个单位，则平移后的点的坐标是(　　)

A. (1，3)
B. (7，7)
C. (1，7)
D. (7，3)

8．从1980年初次征战冬奥会，到1992年取得首枚冬奥会奖牌，再到2022年北京冬奥会金牌榜前三，中国的冰雪体育事业不断取得突破性成绩．历届冬奥会的比赛项目常被分成两大类：冰项目和雪项目．根据统计图提供的信息，有如下四个结论：
①中国队在2022年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次；
②中国队在2022年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次；
③中国队在冬奥会上的冰上项目奖牌数逐年提高；
④中国队在冬奥会上的雪上项目奖牌数在2022年首次超越冰上项目奖牌数．

上述结论中，正确的有(　　)

A. 1个
B. 2个
C. 3个
D. 4个

9．若分式

x

x+1

的值为0，则x的值是．

10．分解因式：2x²-12x+18= ．

11．写一个当x＞0时，y随x的增大而增大的函数解析式．

12．计算：

a

a-2

+

2

2-a

= ．

13．据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验，阐释了光的直线传播原理，如图(1)所示．如图(2)所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是 cm．

14．不透明布袋中有红、黄小球各一个，除颜色外无其他差别．随机摸出一个小球后，放回并摇匀．再随机摸出一个，则两次摸到的球中，一个红球、一个黄球的概率为．

15．如图，在边长为1的正方形网格中，点A，B，D在格点上，以AB为直径的圆过C，D两点，则sin∠BCD的值为．

16．在一次数学活动课上，某数学老师将1～10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下)．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：11；乙：4；丙：15；丁：8；戊：17，则丙同学手里拿的卡片的数字是．

17．计算：(-1)²⁰²²+

3√8

-(

1

3

)^-1+

√2

sin45°．

18．解不等式6-4x≥3x-8，并写出其正整数解．

19．如图，在△ABC中，AB=AC．
求作：直线AD，使得AD∥BC．

小明的作法如下：
①以点A为圆心、适当长为半径画弧，交BA的延长线于点E，交线段AC于点F；
②分别以点E，F为圆心、大于

1

2

EF的长为半径画弧，两弧在∠EAC的内部相交于点D；
③画直线AD．
直线AD即为所求，
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：由作法可知：AD平分∠EAC．
∴∠EAD=∠DAC(       )．(填推理的依据)
∵AB=AC，
∴∠B=∠C
∵∠EAC=∠B+∠C，
∴∠EAC=2∠B．
∵∠EAC=2∠EAD，
∴∠EAD=      ．
∴AD∥BC(       )．(填推理的依据)

20．已知关于x的一元二次方程x²-2kx+k²-1=0．
(1)不解方程，判断此方程根的情况；
(2)若x=2是该方程的一个根，求代数式-2k²+8k+5的值．

21．如图，在平行四边形ABCD中，DB=DA，点F是AB的中点，连接DF并延长，交CB的延长线于点E，连接AE．
(1)求证：四边形AEBD是菱形；
(2)若DC=

√10

，tan∠DCB=3，求菱形AEBD的边长．

22．如图，在平面直角坐标系xOy中，双曲线y=

k

x

(k≠0)经过点A(2，-1)，直线l：y=-2x+b经过点B(2，-2)．
(1)求k，b的值；
(2)过点P(n，0)(n＞0)作垂直于x轴的直线，与双曲线y=

k

x

(k≠0)交于点C，与直线l交于点D．
①当n=2时，判断CD与CP的数量关系；
②当CD≤CP时，结合图象，直接写出n的取值范围．

23．如图，在△ABC中，AB＞AC，∠BAC=90°，在CB上截取CD=CA，过点D作DE⊥AB于点E，连接AD，以点A为圆心、AE的长为半径作⊙A．
(1)求证：BC是⊙A的切线；
(2)若AC=5，BD=3，求DE的长．

24．某研究中心建立了自己的科技创新评估体系，并对2021年中国城市的科技创新水平进行了评估．科技创新综合指数由科技创新总量指数和科技创新效率指数组成(以下简称：综合指数、总量指数和效率指数)．该研究中心对2021年中国城市综合指数得分排名前40的城市的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
a．综合指数得分的频数分布表(数据分成6组：65.0x≤70.0，70.0≤x＜75.0，75.0≤x＜80.0，80.0≤x＜85.085.0≤x＜90.0，90.0≤x＜95.0)：

综合指数得分	频数
65.0x≤70.0	8
70.0≤x＜75.0	16
75.0≤x＜80.0	8
80.0≤x＜85.0	m
85.0≤x＜90.0	2
90.0≤x＜95.0	1
合计	40

b．综合指数得分在70.0≤x＜75.0这一组的是：70.0，70.4，70.6，70.7，71.0，71.0，71.1，71.2，71.8，71.9，72.5，73.8，74.0，74.4，74.5，74.6．
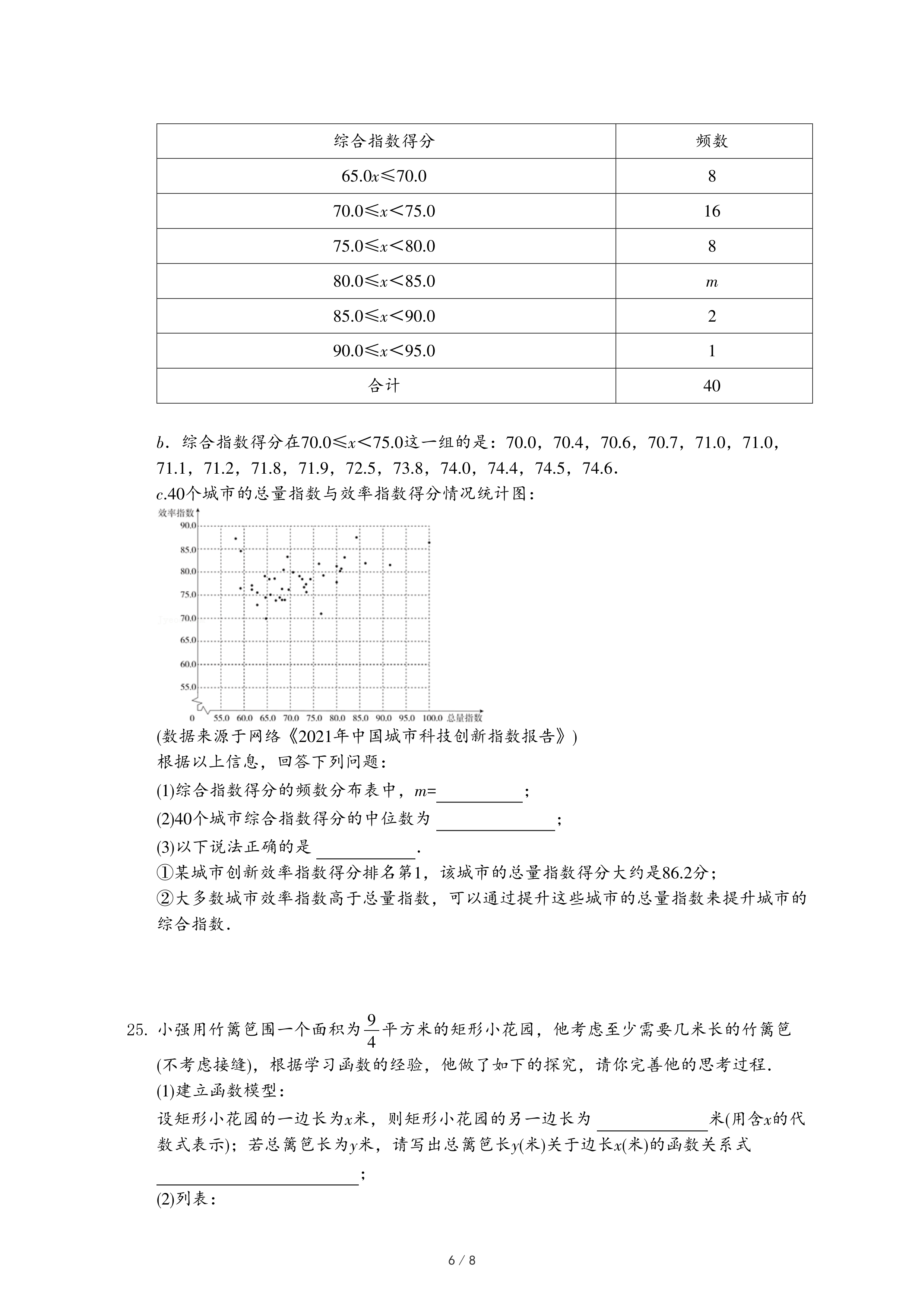
c.40个城市的总量指数与效率指数得分情况统计图：

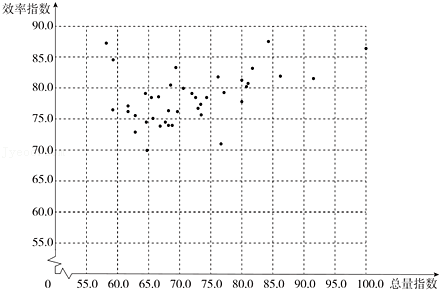
(数据来源于网络《2021年中国城市科技创新指数报告》)
根据以上信息，回答下列问题：
(1)综合指数得分的频数分布表中，m=      ；
(2)40个城市综合指数得分的中位数为       ；
(3)以下说法正确的是       ．
①某城市创新效率指数得分排名第1，该城市的总量指数得分大约是86.2分；
②大多数城市效率指数高于总量指数，可以通过提升这些城市的总量指数来提升城市的综合指数．

25．小强用竹篱笆围一个面积为

9

4

平方米的矩形小花园，他考虑至少需要几米长的竹篱笆(不考虑接缝)，根据学习函数的经验，他做了如下的探究，请你完善他的思考过程．
(1)建立函数模型：
设矩形小花园的一边长为x米，则矩形小花园的另一边长为米(用含x的代数式表示)；若总篱笆长为y米，请写出总篱笆长y(米)关于边长x(米)的函数关系式；
(2)列表：
根据函数的表达式，得到了x与y的几组对应值，如表：

x

1

2

1

3

2

5

2

3

7

2

4

9

2

5

y

10

13

2

6

a

34

5

15

2

58

7

73

8

b

109

10

表中a= ，b= ；
(3)描点、画出函数图象：
如图，在平面直角坐标系xOy中，将表中未描出的点(2，a)，(

9

2

，b)补充完整，并根据描出的点画出该函数的图象；
(4)解决问题：
根据以上信息可得，当x= 时，y有最小值．由此，小强确定篱笆长至少为米．

26．在平面直角坐标系xOy中，抛物线y=ax²+bx+1(a≠0)的对称轴是直线x=3．
(1)直接写出抛物线与y轴的交点坐标；
(2)求抛物线的顶点坐标(用含a的式子表示)；
(3)若抛物线与x轴相交于A，B两点，且AB≤4，求a的取值范围．

27．如图，在△ABC中，AB=AC，∠CAB=2α，在△ABC的外侧作直线AP(90°-a＜∠PAC＜180°-2a)，作点C关于直线AP的对称点D，连接AD，BD，BD交直线AP于点E．
(1)依题意补全图形；
(2)连接CE，求证：∠ACE=∠ABE；
(3)过点A作AF⊥CE于点F，用等式表示线段BE，2EF，DE之间的数量关系，并证明．

28．在平面直角坐标系xOy中，对于图形G及过定点P(3，0)的直线l，有如下定义：过图形G上任意一点Q作QH⊥l于点H，若QH+PH有最大值，那么称这个最大值为图形G关于直线l的最佳射影距离，记作d(G，l)，此时点Q称为图形G关于直线l的最佳射影点．
(1)如图1，已知A(2，2)，B(3，3)，写出线段AB关于x轴的最佳射影距离d(AB，x轴)= ；
(2)已知点C(3，2)，⊙C的半径为

√2

，求⊙C关于x轴的最佳射影距离d(⊙C，x轴)，并写出此时⊙C关于x轴的最佳射影点Q的坐标；
(3)直接写出点D(0，

√3

)关于直线l的最佳射影距离d(点D，l)的最大值．