2022年北京市朝阳区中考数学一模试卷-乐乐课堂

1．如图是某几何体的三视图，该几何体是(　　)

A. 三棱柱
B. 长方体
C. 圆锥
D. 圆柱

2．2022年3月5日，国务院总理李克强代表国务院，向十三届全国人大五次会议作政府工作报告．报告中指出过去一年是党和国家历史上具有里程碑意义的一年，“十四五”实现良好开局，我国发展又取得新的重大成就.2021年国内生产总值达114万亿元，增长8.1%．将1140000用科学记数法表示应为(　　)

A. 0.114×10⁷
B. 1.14×10⁵
C. 1.14×10⁶
D. 11.4×10⁴

3．实数a，b在数轴上对应的点的位置如图所示，下列结论中正确的是(　　)

A. a+b＞0
B. ab＞0
C. a-b＞0
D. |a|＞|b|

4．将一副三角尺(厚度不计)如图摆放，使有刻度的两条边互相平行，则图中∠1的大小为(　　)

A. 100°
B. 105°
C. 115°
D. 120°

5．下列多边形中，内角和与外角和相等的是(　　)

A.
B.
C.
D.

6．不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，两次都摸到颜色相同的球的概率为(　　)

A.
2
3
B.
1
3
C.
1
2
D.
1
4

7．如图是国家统计局公布的2021年居民消费价格月度涨跌幅度，月度同比和月度环比的平均数分别为x_同，x_环，方差分别为s_同²，s_环²，则(　　)

A. x_同＞x_环，s_同²＞s_环²
B. x_同＞x_环，s_同²＜s_环²
C. x_同＜x_环，s_同²＞s_环²
D. x_同＜x_环，s_同²＜s_环²

8．点A(x₁，y₁)，B(x₂，y₂)在反比例函数y=

2

x

的图象上，下列推断正确的是(　　)

A. 若x₁＜x₂，则y₁＜y₂
B. 若x₁＜x₂，则y₁＞y₂
C. 若x₁+x₂=0，则y₁+y₂=0
D. 存在x₁=x₂使得y₁≠y₂

9．若代数式

1

x-1

有意义，则实数x的取值范围是．

10．分解因式：2a²-4ab+2b²= ．

11．写出一个比4大且比5小的无理数：．

12．如图，AC、BC是⊙O的弦，PA、PB是⊙O的切线，若∠C=60°，则∠P= ．

13．如图，在△ABC中，AB=AC，点D在AC上(不与点A，C重合)，只需添加一个条件即可证明△ABC和△BDC相似，这个条件可以是 (写出一个即可)．

14．如图，2022年北京冬奥会上，一些可看作正六边形的“小雪花”对称地排列在主火炬周围，中间空出了13个“小雪花”的位置来突出主火炬．在其中91个“小雪花”上面写有此次参会的国家或地区的名称，此外还有几个“小雪花”上面只有中国结图案．这些只有中国结图案的“小雪花”共有个．

15．若关于x的一元二次方程(a-1)x²+a²x-a=0有一个根是x=1，则a的值为．

16．尊老敬老是中华民族的传统美德，某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出，他们一共准备了6个节目，全体演员中有8人需参加两个或两个以上的节目演出，情况如表：

	演员1	演员2	演员3	演员4	演员5	演员6	演员7	演员8
节目A	√		√		√	√		√
节目B	√		√	√
节目C				√		√		√
节目D		√			√
节目E		√					√
节目F					√		√

从演员换装的角度考虑，每位演员不能连续参加两个节目的演出，从节目安排的角度考虑，首尾两个节目分别是A，F，中间节目的顺序可以调换，请写出一种符合条件的节目先后顺序 (只需按演出顺序填写中间4个节目的字母即可)．

17．计算：2cos30°+|-

√3

|-(π-

√3

)⁰-

√12

．

18．解不等式组：．

19．已知x²+x-3=0，求代数式(2x+3)(2x-3)-x(x-3)的值．

20．已知关于x的一元二次方程x²-ax+a-1=0．
(1)求证：该方程总有两个实数根；
(2)若该方程的两个实数根都是整数，且其中一个根是另一个根的2倍，求a的值．

21．中国古代数学家李子金在《几何易简集》中记载了圆内接正三角形的一种作法：“以半径为度，任用圆界一点为心，作两圆相交，又移一心，以交线为界，再作一交圆，其三线相交处为一角，其两线相交处为两角，直线界之亦得所求”．
由记载可得作法如下：
①作⊙M，在⊙M上取一点N，以点N为圆心，MN为半径作⊙N，两圆相交于A，B两点，连接AB；
②以点B为圆心，AB为半径作⊙B，与⊙M相交于点C，与⊙N相交于点D；
③连接AC，AD，BC，BD．
△ABC，△ABD都是圆内接正三角形．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连接AM，AN，MN，BM．
∵MA=MN=NA，
∴△AMN为．
∴∠AMN=60°．
同理可得，∠BMN=60°．
∴∠AMB=120°．
∴∠ACB=60°( )(填推理的依据)．
∵BA=BC，
∴△ABC是等边三角形．
同理可得，△ABD是等边三角形．

22．如图，在矩形ABCD中，AC，BD相交于点O，AE∥BD，BE∥AC．
(1)求证：四边形AEBO是菱形；
(2)若AB=OB=2，求四边形AEBO的面积．

23．如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．
(1)求证：AC平分∠DAB；
(2)若cos∠CAD=

4

5

，AB=5，求CD的长．

24．某公园在人工湖里建造一道喷泉拱门，工人在垂直于湖面的立柱上安装喷头，从喷头喷出的水柱的形状可以看作是抛物线的一部分．安装后，通过测量获得如下数据，喷头高出湖面3米，在距立柱水平距离为d米的地点，水柱距离湖面高度为h米．

d(米)	0.50	1.00	1.50	2.00	2.50	3.00
h(米)	3.75	4.00	3.75	3.00	1.75	0

请解决以下问题：
(1)在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；
(2)结合表中所给数据或所画图象，直接写出水柱最高点距离湖面的高度；
(3)求h关于d的函数表达式；
(4)公园希望游船能从喷泉拱门下穿过，已知游船的宽度约为2米，游船的平顶棚到湖面的高度约为1米，从安全的角度考虑，要求游船到立柱的水平距离不小于1米，顶棚到水柱的竖直距离也不小于1米．工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求，请通过计算说明应如何调整．

25．某校初三年级有两个校区，其中甲校区有200名学生，乙校区有300名学生，两个校区所有学生都参加了一次环保知识竞赛，为了解两个校区学生的答题情况，进行了抽样调查，从甲、乙两个校区各随机抽取20名学生，对他们本次环保知识竞赛的成绩(百分制)进行了整理、描述和分析．下面给出了部分信息．
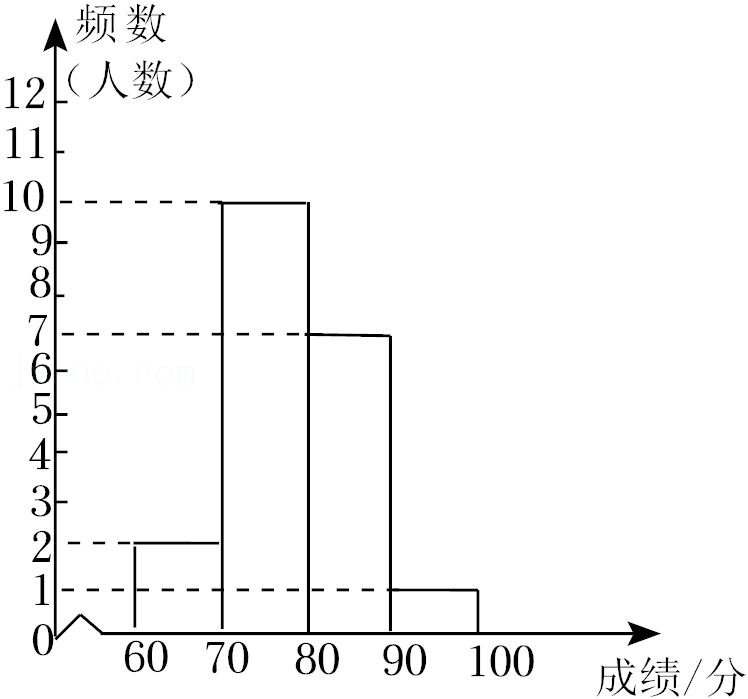
a．甲校区成绩的频数分布直方图如下(数据分成4组：60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100)：
b．甲校区成绩在70≤x＜80这一组的是：74 74 75 77 77 77 77 78 79 79
c．甲、乙两校区成绩的平均数、中位数如下：

	平均数	中位数
甲校区	79.5	m
乙校区	77	81.5

根据以上信息，回答下列问题：
(1)写出表中m的值；
(2)两个校区分别对本次抽取的学生的成绩进行等级赋分，超过本校区的平均分就可以赋予等级A，判断在本次抽取的学生中哪个校区赋予等级A的学生更多，并说明理由；
(3)估计该校初三年级所有学生本次环保知识竞赛的平均分为 (直接写出结果)．

26．在平面直角坐标系xOy中，点(-2，0)，(-1，y₁)，(1，y₂)，(2，y₃)在抛物线y=x²+bx+c上．
(1)若y₁=y₂，求y₃的值；
(2)若y₂＜y₁＜y₃，求y₃的取值范围．

27．在△ABC中，D是BC的中点，且∠BAD≠90°，将线段AB沿AD所在直线翻折，得到线段AB'，作CE∥AB交直线AB'于点E．
(1)如图，若AB＞AC，
①依题意补全图形；
②用等式表示线段AB，AE，CE之间的数量关系，并证明；
(2)若AB＜AC，上述结论是否仍然成立？若成立，简述理由；若不成立，直接用等式表示线段AB，AE，CE之间新的数量关系(不需证明)．

28．在平面直角坐标系xOy中，对于直线l：y=kx+b，给出如下定义：若直线l与某个圆相交，则两个交点之间的距离称为直线l关于该圆的“圆截距”．
(1)如图1，⊙O的半径为1，当k=1，b=1时，直接写出直线l关于⊙O的“圆截距”；
(2)点M的坐标为(1，0)，
①如图2，若⊙M的半径为1，当b=1时，直线l关于⊙M的“圆截距”小于

4

5

√5

，求k的取值范围；
②如图3，若⊙M的半径为2，当k的取值在实数范围内变化时，直线l关于⊙M的“圆截距”的最小值2，直接写出b的值．

【2022年北京市朝阳区中考数学一模试卷】-第3页