9．若式子在实数范围内有意义，则x的取值范围是      ．

10．若a²-2a=1，则3a²-6a+5=      ．

11．已知二次函数y=ax²+bx+c(a、b、c为常数，且a≠0)的y与x的部分对应值如下表：

则关于x的一元二次方程ax²+bx+c=0的根是       ．

12．如图，正方形ABCD的对角线AC与BD相交于点O，以点C为圆心，适当长为半径画弧，分别交AC，BC于点E、F，分别以点E、F为圆心，大于EF长为半径画弧，两弧交于点G，连接CG，并延长交DB于M点，若BM=，则线段OM=      ．

13．某工程队承接了80万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前20天完成了任务，则原计划每天绿化的面积为多少万平方米．设原计划每天绿化的面积为x万平方米，依题意可列方程       ．

14．如图，某校教学楼后面紧邻着一个山坡，坡上面是一块平地．BC∥AD，斜坡AB长26m，斜坡AB的坡度为12：5，为了减缓坡面，防止山体滑坡，学校决定对该斜坡进行改造，经地质人员勘测，当坡角不超过53°时，可确保山体不滑坡．如果改造时保持坡脚A不动，则坡顶B沿BC至少向右移动       m时，才能确保山体不滑坡．(取tan53°≈)

15．在平面直角坐标系中，直角△AOB如图放置，点A的坐标为(1，0)，∠AOB=60°，每一次将△AOB绕点O逆时针旋转90°，第一次旋转后得到△A₁OB₁，第二次旋转后得到△A₂OB₂，依次类推，则点B₂₀₂₂的坐标为       ．

16．如图，在矩形ABCD中，AB=4，BC=6，E是BC的中点，连接AE，P是边AD上一动点，沿过点P的直线将矩形折叠，使点D落在AE上的点D′处，当△APD′是直角三角形时，PD=      ．

17．计算：|1-|-2cos45°+(π-3.14)⁰+()^-1．

18．如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上，连接DB．
(1)证明：△ACE≌△BCD；
(2)若AE=1，AD=2，求AC的长．

19．我市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一外型、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶，为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如图所示的两幅不完整的统计图．
根据图中信息，解答下列问题：
(1)此次调查共随机采访了________名学生，在扇形统计图中“灰”所在扇形的圆心角的度数为 ________度，补全条形统计图(要求在条形图上方注明人数)；
(2)若该校有2400名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；
(3)李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图或列表法求出恰好抽中A，B两人的概率．

20．如图，一次函数y=k₁x+b(k₁≠0)与反比例函数y=(k₂≠0)的图象交于点A(2，3)，B(a，-1)，设直线AB交x轴于点C．
(1)求反比例函数和一次函数的解析式．
(2)直接写出k₁x+b＜的解集．
(3)若点P是反比例函数图象上的一点，且△POC是以OC为底边的等腰三角形，求P点的坐标．

21．如图，△ABC内接于⊙O，AB是⊙O的直径，AD是⊙O的切线，点A为切点，AD=AC，连接DC交AB于点E．
(1)求证，BC=BE．
(2)若tan∠ACE=，AB=5，求BC的长．

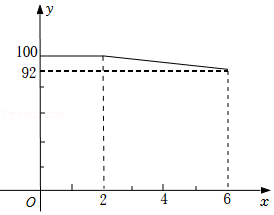
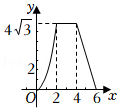
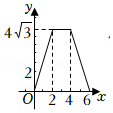
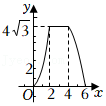
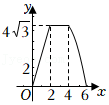
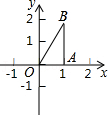22．某公司生产的一种产品在市场上很受欢迎，该公司每年的产量为6万件，可在国内和国外两个市场全部销售．若在国外销售，平均每件产品的利润y₁(元)与国外销售量x(万件)之间的函数关系如图所示．若在国内销售，平均每件产品的利润为y₂=84元，设该公司每年在国内和国外销售的总利润为w万元．
(1)求y₁与x之间的函数关系式，并求x的取值范围．
(2)该公司每年在国内国外销售量各为多少时，可使公司每年的总利润最大？最大值是多少？
(3)该公司计划以国外销售的每件产品中捐出2m(1≤m≤4)元给希望工程，从国内销售的每件产品中捐出m元给希望工程，且国内销售量不低于4万件，若这时国内外销售的总利润的最大值为520万元，求m的值．

23．如图，在等腰△ABC中，∠BAC=α，AB=AC，点D是边BC上的动点，连接AD，将△ADC绕点A顺时针旋转α得到△AFB，连FD交AB于点E．
(1)问题探究：
①先将问题特殊化，如图1，当∠α=60°，点D是BC的中点时，则=    =    ．
②再将问题一般化，如图2，当∠BAC=α，D是BC边上任一点，求证：=．
(2)问题拓展：
如图3，若AB=AC=5，BC=6，点M为AB的中点，连接MF，在D点的运动过程中，直接写出MF的最小值．

24．如图，已知抛物线y=ax²+bx+3与x轴交于点A(-1，0)和点B(3，0)，与y轴交于点C，连接AC．
(1)求该抛物线的解析式；
(2)若点P是该抛物线上一点，且∠PAB=∠ACO，求P点的坐标．
(3)若经过A、C两点的圆M与该抛物线的对称轴相切，求圆心M的坐标．