13．(1)计算：|1-|-2sin45°+2^-1．
(2)已知：如图，在▱ABCD中，AC为对角线，∠BAC=∠DAC．求证：▱ABCD为菱形．

14．先化简，再求值：÷，其中实数m可使关于x的一元二次方程x²-4x-m=0有两个相等的实数根．

15．为弘扬中国传统文化，某校举办了中小学生“国学经典大赛”，比赛项目为：A．唐诗，B．宋词，C．论语，D．三字经．比赛形式为“单人组”和“双人组”．
(1)小颖参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“论语”的概率为    ；
(2)若“双人组”比赛规则是：同一小组的两名成员的比赛项目不能相同，且每人只能随机抽取一次，则小明和小峰组成的“双人组”恰好有一人是唐诗，另一人是宋词的概率是多少？请用画树状图或列表的方法进行说明．

16．如图，正六边形ABCDEF在正三角形网格内，点O为正六边形的中心，仅用无刻度的直尺完成以下作图．
(1)在图1中，过点O作AC的平行线；
(2)在图2中，过点E作AC的平行线．

17．为全力抗战疫情，响应政府“停课不停学”的号召，某市教育局发布关于疫情防控期间开展在线课程教学的通知：从2月10日开始，全市中小学按照教学计划，开展在线课程教学和答疑．某校九年级想了解该年级学生对“在线课程教学和答疑”的满意程度，随机抽取了部分学生进行问卷，问卷有以下四个选项：A．十分满意，B．满意，C．比较满意，D．不满意(要求每名学生选且只能选一项)，现将调查的结果统计如下，根据图表信息解决下列问题．

(1)本次一共抽取了________名学生，并补全条形图；
(2)扇形图中，“十分满意”对应扇形的圆心角为      ；
(3)若该年级共有2000名学生，请问该年级共有多少学生对这次教学是“满意”和“十分满意”的．

18．如图，PA是⊙O的切线，点A为切点，⊙O与线段OP相交于点B，点C是线段AP上一点，连接OC，CB．
(1)当OC是△OAP的________时，CB是⊙O的切线(请填下列序号，并加以证明)；
①中线，②角平分线，③高线
(2)在(1)的条件下，若OA=6，AP=8，求切线CB的长．

19．在抗击新型冠状病毒期间，科学合理调运各种防控物资是重要任务之一．在某市的甲、乙、丙、丁四地中，已知某种消毒液甲地需要10吨，乙地需要8吨，正好丙地储备有12吨，丁地储备有6吨．该市新冠肺炎疫情防控应急指挥部决定将这18吨消毒液全部调往甲、乙两地．已知消毒液的运费价格如下表(单位：元/吨)．又知从丙地调运2吨到甲地、3吨到乙地共需420元；从丙地调运4吨到甲地、2吨到乙地共需440元．如果设从丙地调运x吨到甲地．
(1)确定表中a，b的值；
(2)求调运18吨消毒液的总运费y关于x的函数关系式；
(3)求出总运费最低的调运方案，并求出最低运费是多少．

20．如图，直角△ABC中，∠C=90°，AC=2，BC=4，AC平行于x轴，A、B两点在反比例函数y=(x＞0)的图象上．延长CA交y轴于点D，AD=1．
(1)求反比例函数的解析式；
(2)在y轴上是否存在点P，使△PAB的周长最小，若存在，求出点P的坐标并直接写出此时△PAB的周长；若不存在，说明理由．

21．如图是一种电脑桌，其实物图如图1所示，此电脑桌的桌面可调节，图2和图3是其可调节桌面的侧面示意图，在点C处固定安装了一根长度一定的支撑臂CB．点B可在AD上滑动，AC=25cm．(其中(2)，(3)两问结果保留小数点后一位)
(1)在图2中，当BC⊥AC时，测得∠BAC=45°，求支撑臂CB的长；
(2)在图3中，当BC与AC不垂直时，测得∠BAC=22°，求此时AB的长；
(3)从图2到图3过程中，求点C在此运动过程中的路径长．
(参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，π≈3.14)

22．定义：如果三角形的一个内角是另一个内角的2倍，那么称这个三角形为“倍角三角形”．
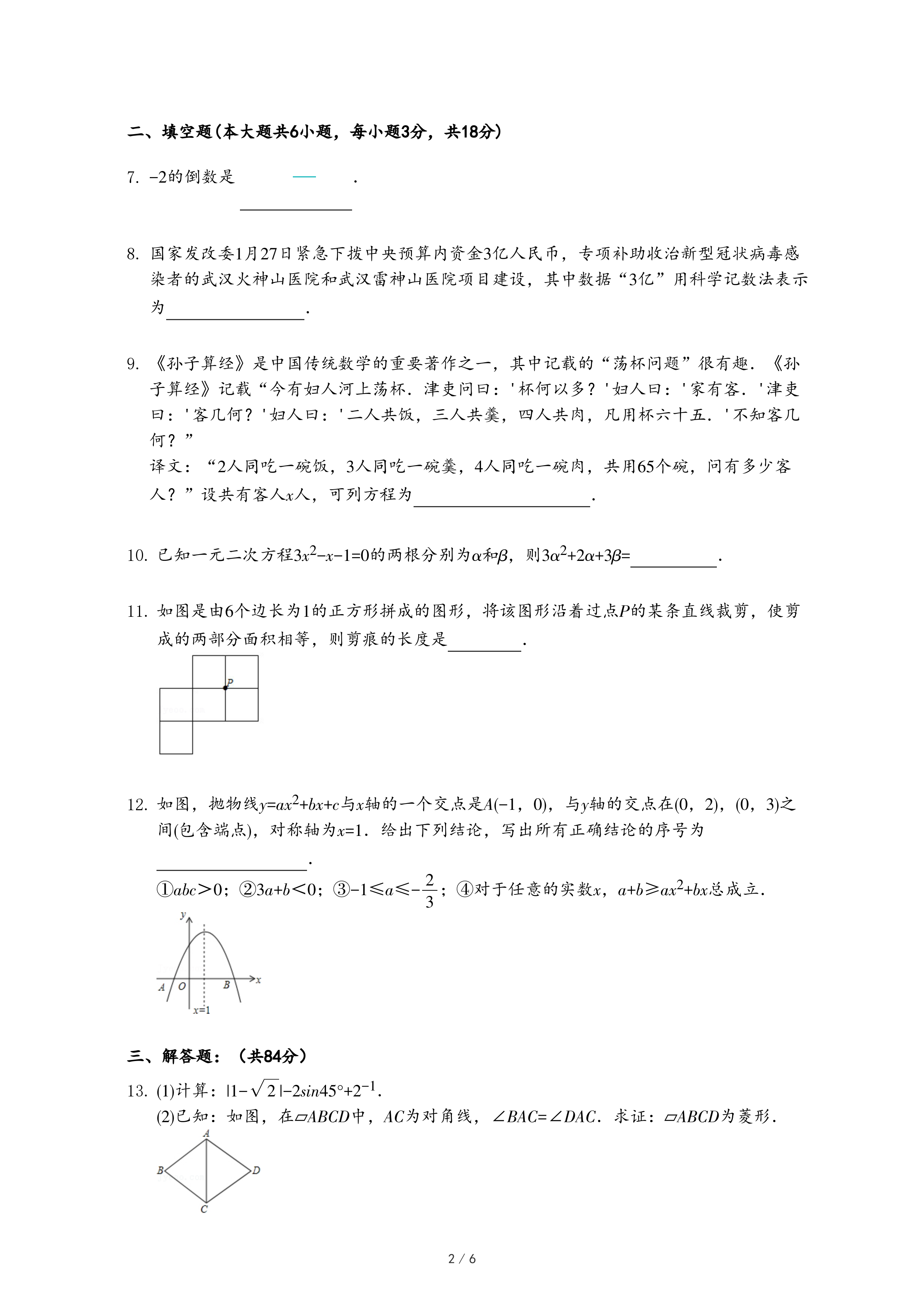
如图①，在△ABC中，∠A=80°，∠B=40°，那么△ABC就是一个“倍角三角形”．
[定义应用]
(1)已知△ABC是倍角三角形，∠A=60°．则这个三角形其余两个内角的度数分别为      ．
[性质探究]
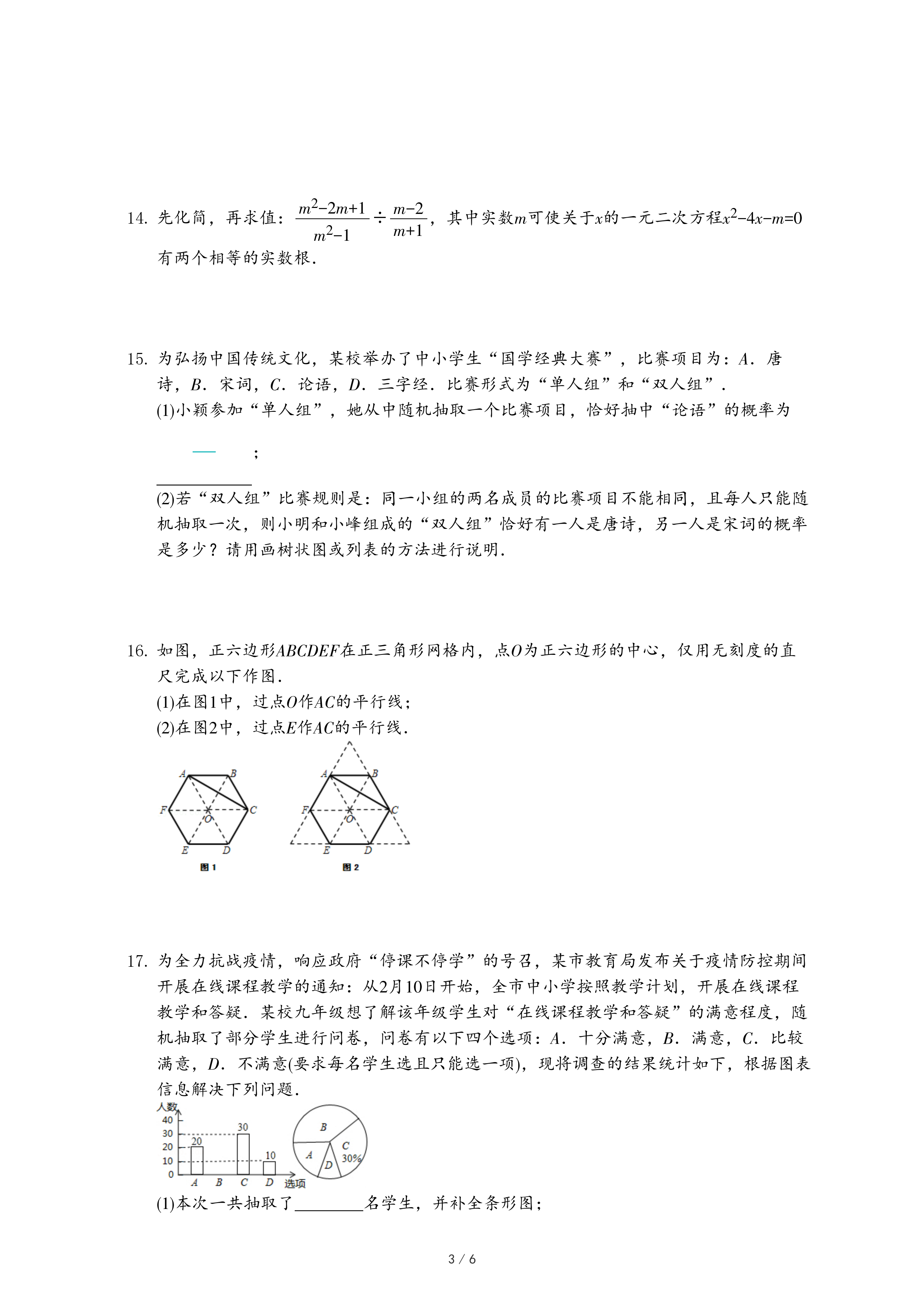
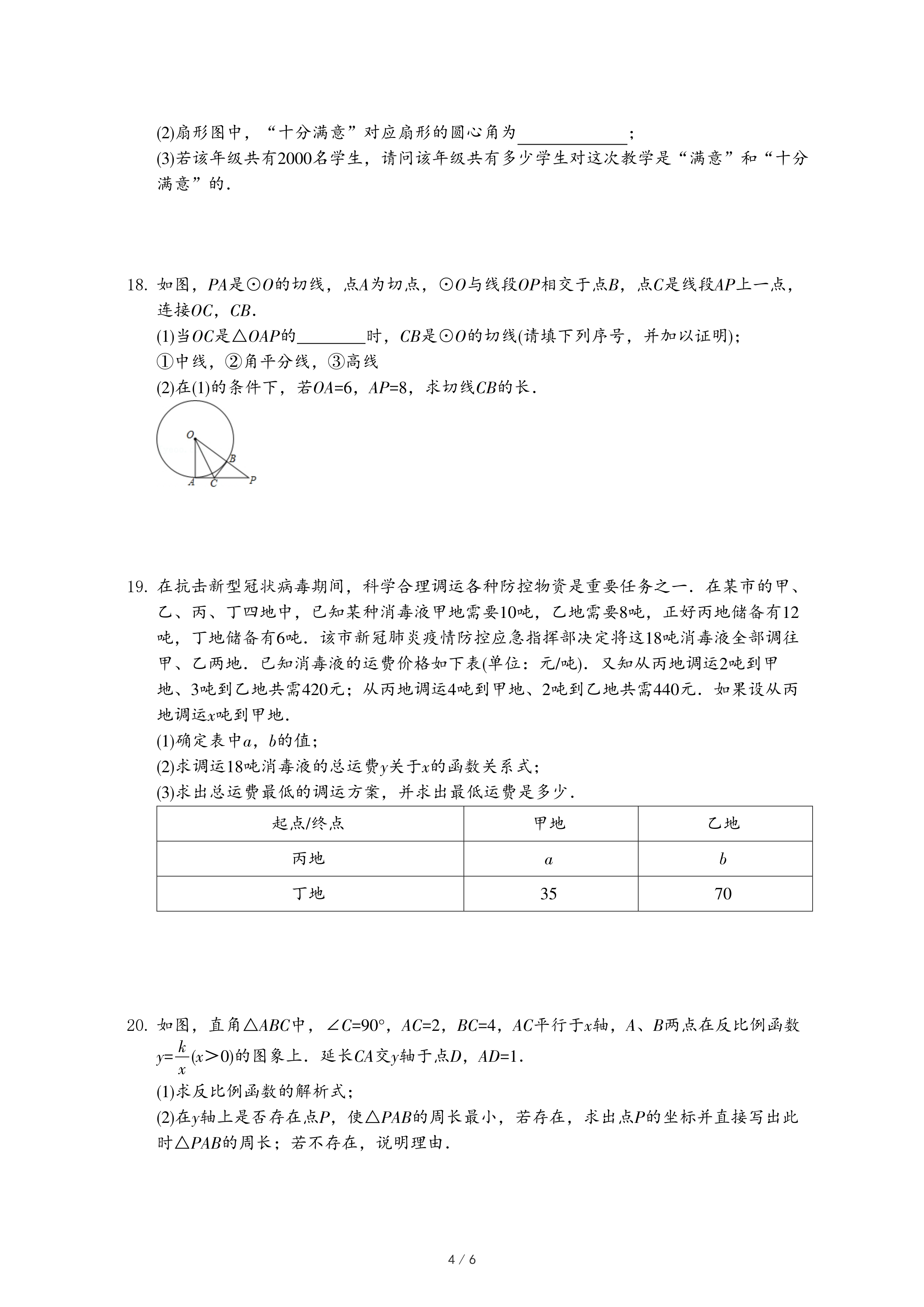
(2)在△ABC中，∠A，∠B，∠C所对边的边长分别为a，b，c．若∠A=2∠B，且∠A=60°，如图②，易得到a²=b(b+c)．那么在任意的△ABC中，满足∠A=2∠B，如图③，关系式a²=b(b+c)是否仍然成立？若成立，请加以证明；若不成立，请说明理由．
[拓展应用]
(3)若一等腰三角形恰好是一个倍角三角形，求它的腰与底边之比．

23．已知抛物线C₁：y=ax²+bx+(a≠0)经过点A(-1，0)和B(3，0)．
(1)求抛物线C₁的解析式，并写出其顶点C的坐标；
(2)如图1，把抛物线C₁沿着直线AC方向平移到某处时得到抛物线C₂，此时点A，C分别平移到点D，E处．设点F在抛物线C₁上且在x轴的下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标；
(3)如图2，在(2)的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：①tan∠ENM的值如何变化？请说明理由；②点M到达点C时，直接写出点P经过的路线长．