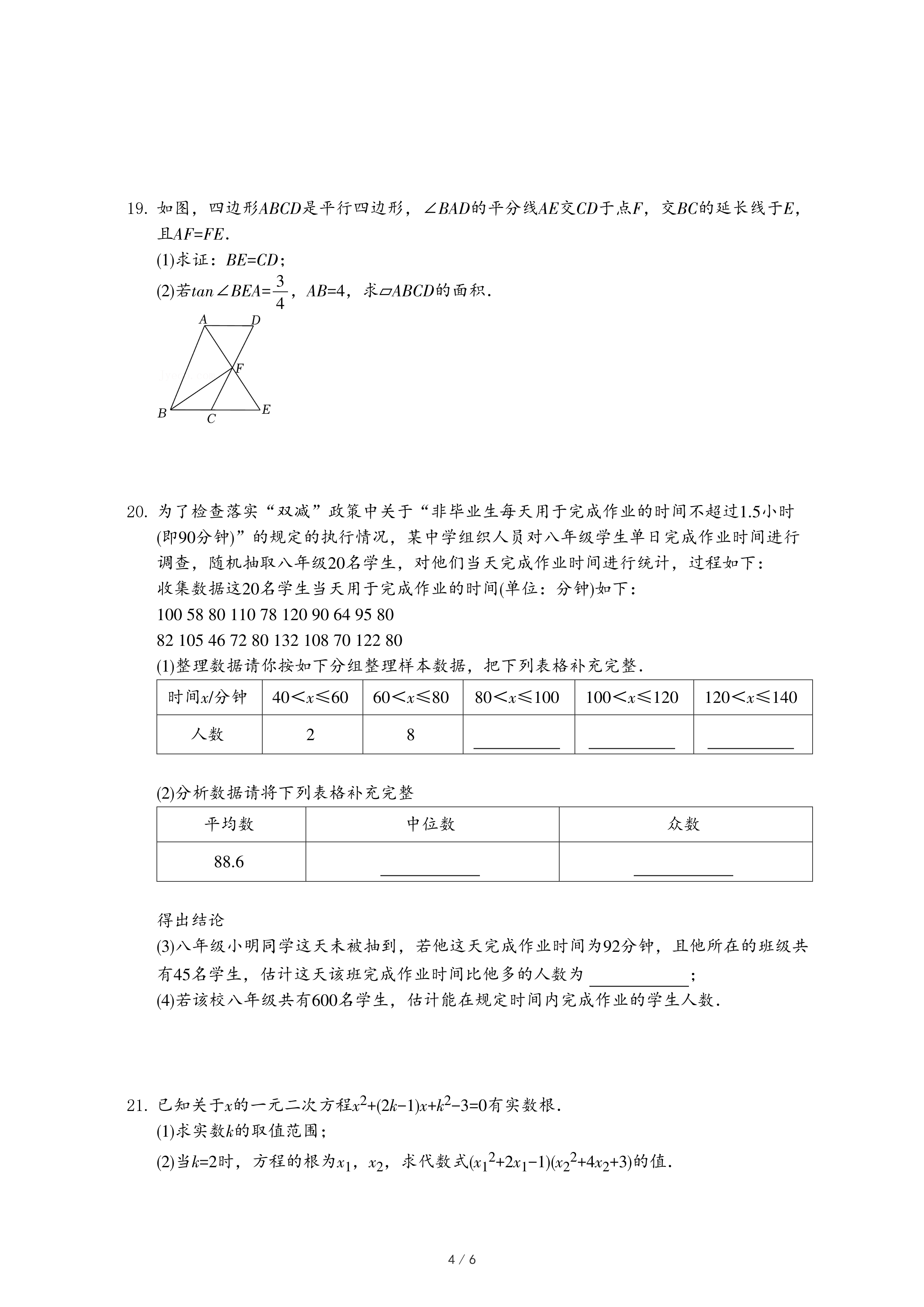
20.为了检查落实“双减”政策中关于“非毕业生每天用于完成作业的时间不超过1.5小时(即90分钟)”的规定的执行情况,某中学组织人员对八年级学生单日完成作业时间进行调查,随机抽取八年级20名学生,对他们当天完成作业时间进行统计,过程如下:
收集数据这20名学生当天用于完成作业的时间(单位:分钟)如下:
100 58 80 110 78 120 90 64 95 80
82 105 46 72 80 132 108 70 122 80
(1)整理数据请你按如下分组整理样本数据,把下列表格补充完整.
| 时间x/分钟 | 40<x≤60 | 60<x≤80 | 80<x≤100 | 100<x≤120 | 120<x≤140 |
| 人数 | 2 | 8 | | | |
(2)分析数据请将下列表格补充完整
得出结论
(3)八年级小明同学这天未被抽到,若他这天完成作业时间为92分钟,且他所在的班级共有45名学生,估计这天该班完成作业时间比他多的人数为
;
(4)若该校八年级共有600名学生,估计能在规定时间内完成作业的学生人数.