24.在平面直角坐标系xOy中,已知P(x
1,y
1)Q(x
2,y
2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x
2-x
1|+|y
2-y
1|
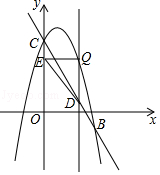
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5-1|+|2-4|=6.
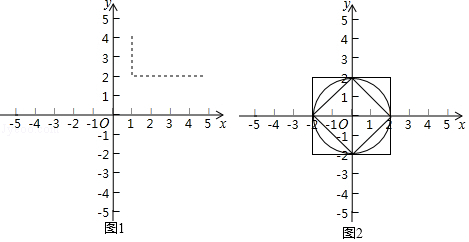

(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号
.
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.