18．计算：2cos30°+|-|+()^-2-．

19．已知：如图，∠MAN=90°，线段a和线段b
求作：矩形ABCD，使得矩形ABCD的两条边长分别等于线段a和线段b．
下面是小东设计的尺规作图过程．
作法：如图，
①以点A为圆心，b为半径作弧，交AN于点B；
②以点A为圆心，a为半径作弧，交AM于点D；
③分别以点B、点D为圆心，a、b长为半径作弧，两弧交于∠MAN内部的点C；
④分别连接BC，DC．
所以四边形ABCD就是所求作的矩形．
根据小东设计的尺规作图过程，
(1)使用直尺和圆规，补全图形；(保留作图痕迹)

(2)完成下面的证明．
证明：
∵AB=      ；AD=      ；
∴四边形ABCD是平行四边形．
∵∠MAN=90°；
∴四边形ABCD是矩形(填依据      )．

20．如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AB∥CD，AE=DF，∠A=∠D．
(1)求证：AB=CD；
(2)若AB=CF，∠B=40°，求∠D的度数．

21．为了丰富学生的业余文化生活，某校教务处准备在大课间期间开设兴趣小组，预设科目为“舞蹈”“音乐”“电竞”“动漫”为了准确配备教室与师资，负责人制作了“你最喜欢的科目”的调查问卷，在校园随机调查后制作了两幅不完整的统计图，请你根据信息解答下面问题：

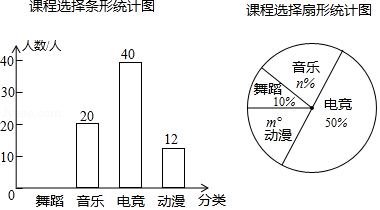
(1)本次调查中，参与问卷调查的人数为      ；
(2)扇形统计图中的m、n的值为      、      ，补全条形统计图；
(3)若该校有学生2000人，请你估计报名“电竞”的学生的人数为      ；
(4)最先报名“动漫”课程的三名学生中有两名男生一名女生，若随机抽取两名学生参与教室网线布设，求两名学生恰为一男一女的概率．

22．如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作AE⊥CD，交CD的延长线于点E，DA平分∠BDE．
(1)求证：AE是⊙O的切线；
(2)已知AE=8cm，CD=12cm，求⊙O的半径．

23．如图，在△ABC与△EBD中，∠ABC=∠EBD=90°，AB=6，BC=3，EB=2，BD=，射线AE与直线CD交于点P．
(1)求证：△ABE∽△CBD；
(2)若AB∥ED，求tan∠PAC的值；
(3)若△EBD绕点B逆时针旋转一周，直接写出线段AP的最大值与最小值．

24．已知，抛物线y=-x²+bx+c交y轴于点C(0，2)，经过点Q(2，2)．直线y=x+4分别交x轴、y轴于点B、A．

(1)求抛物线的解析式；
(2)如图1，点P为抛物线上一动点(不与点C重合)，PO交抛物线于M，PC交AB于N，连MN．求证：MN∥y轴；
(3)如图2，过点A的直线交抛物线于D、E，QD、QE分别交y轴于G、H．求证：CG•CH为定值．