


| 1 |
| 3 |
| 1 |
| 3 |
| { | x-y=1 2x+y=5 |
| { | x=2 y=1 |
| { | x=-1 y=2 |
| { | x=-2 y=-1 |
| { | x=2 y=-1 |
| 会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
| A类 | 40 | 1年 | 每杯打九折 |
| B类 | 80 | 1年 | 每杯打八折 |
| C类 | 130 | 1年 | 一次性购买2杯,第二杯半价 |
| 1-x |
| x |
| 抛掷次数n | 300 | 500 | 700 | 900 | 1100 | 1300 | 1500 | 1700 | 1900 | 2000 | ||
| “正面向上”的次数m | 137 | 233 | 335 | 441 | 544 | 650 | 749 | 852 | 946 | 1004 | ||
“正面向上”的频率
| 0.457 | 0.466 | 0.479 | 0.490 | 0.495 | 0.500 | 0.499 | 0.501 | 0.498 | 0.502 |
| 甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
| 乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
| { | 4(x+1)≤2x+6 x-3<
|

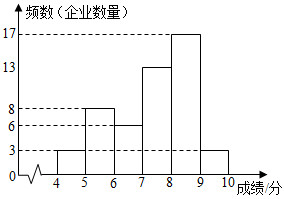
| 平均数 | 中位数 | 众数 | |
| A项指标成绩 | 7.37 | m | 8.2 |
| B项指标成绩 | 7.21 | 7.3 | 8 |
| 4 |
| 3 |
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y1/cm | 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| y2/cm | 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
| 1 |
| 3 |
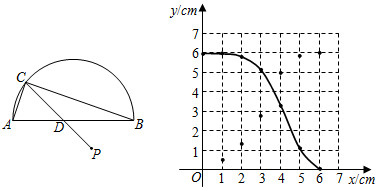
| 1 |
| 2 |

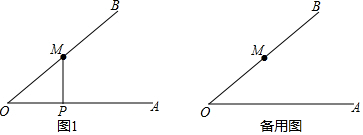
√3 |
| 3 |