17.期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
【收集数据】
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有
;(只要填写序号即可)
①随机抽取一个班级的48名学生;
②在全年级学生中随机抽取48名学生;
③在全年级12个班中分别各抽取4名学生;
④从全年级学生中随机抽取48名男生;
【整理数据】
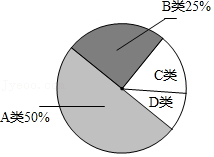
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为
、
.
②估计全年级A、B类学生大约一共有
名;
| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | | 0.5 |
| B类(60~79) | | 0.25 |
| C类(40~59) | 8 | |
| D类(0~39) | 4 | |
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校的教学效果较好?结合数据,请给出一个解释来支持你的观点.