17．已知关于x的一元二次方程x²-2x+m=2有两个不相等的实数根．
（1）求m的取值范围；
（2）当m=1时，求方程x²-2x+m=2的解．

18．电视台为了开展线上“百人合唱一首歌”的“云演出”活动，需招募青少年歌手．甲、乙、丙、丁报名参加了应聘活动，其中甲、乙为男歌手，丙、丁为女歌手．现对这四名歌手采取随机抽取的方式进行线上面试．
（1）若随机抽取一名歌手，求恰好抽到丁的概率；
（2）若随机抽取两名歌手，请用列表或画树状图表示所有可能的结果，并求出恰好抽到一男一女的概率．

19．如图，反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于A(1，a)，B两点．
(1)求反比例函数的解析式；
(2)求不等式>2x的解集．

20．桃园大桥是随州城区第二座景观桥，远远望去，桥身的红色立柱像四根大火炬．如图，小刚利用学到的数学知识测量大桥立柱在水面以上的高度MN．在桥面观测点A处测得某根立柱顶端M的仰角为30°，测得这根立柱与水面交汇点N的俯角为15°，向立柱方向走40米到达观测点B处，测得同一根立柱顶端M的仰角为60°．已知点A，B，C，M，N在同一平面内，桥面与水面平行，且MN垂直于桥面．
（1）求大桥立柱在桥面以上的高度MC（结果保留根号）；
（2）求大桥立柱在水面以上的高度MN（结果精确到1米）．
（参考数据：sin15°≈0.26，cos15°≈0.96，tan15°≈0.27，≈1.73）

21．如图，已知⊙O的直径CD=6，A，B为圆周上两点，且四边形OABC是平行四边形．过A点作直线EF//BD，分别交CD，CB的延长线于点E，F，AO与BD交于G点，
（1）求证：EF是⊙O的切线；
（2）求EF的长．

22．某商家采取线上和线下两种方式销售某款商品，规定无论是线上还是线下每件售价不低于进价，且线上售价始终比线下每件便宜2元．已知该款商品进价为10元/件，线上的月销售量固定为400件，线下的月销售量y（件)与线下售价x（元/件）满足关系式y=-100x+2400．设该商品线上和线下月销售利润总和为W（元）．
（1）求W与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）若该商家每月想从这种商品销售中获得4800元的利润，又想尽量给客户实惠，该如何给这种商品进行线下定价？
（3）物价部门规定，该商品的每件利润不得高于进价的60%，如果商家每月要想从这种商品销售中获得最大利润，他应该把这种商品的线下售价定为多少？月最大销售利润是多少？

23．定义：在一个三角形中，如果一个内角是另一内角的2倍，我们称这样的三角形为“倍角三角形”，把这个2倍角的平分线（线段）称为这个三角形的“伴线”．在倍角△ABC中，∠A=2∠B，∠A的平分线就是它的“伴线”，用a，b，c分别表示∠A，∠B，∠C的对边，现在我们探究a，b，c之间存在的数量关系．
（1）【特例探究】（补全填空）
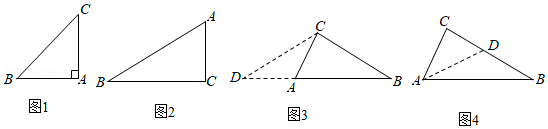
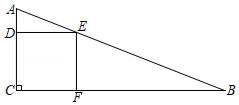
如图1，若∠A=2∠B=90°，b=1，易求得a²-b²的值为1，bc的值为1；
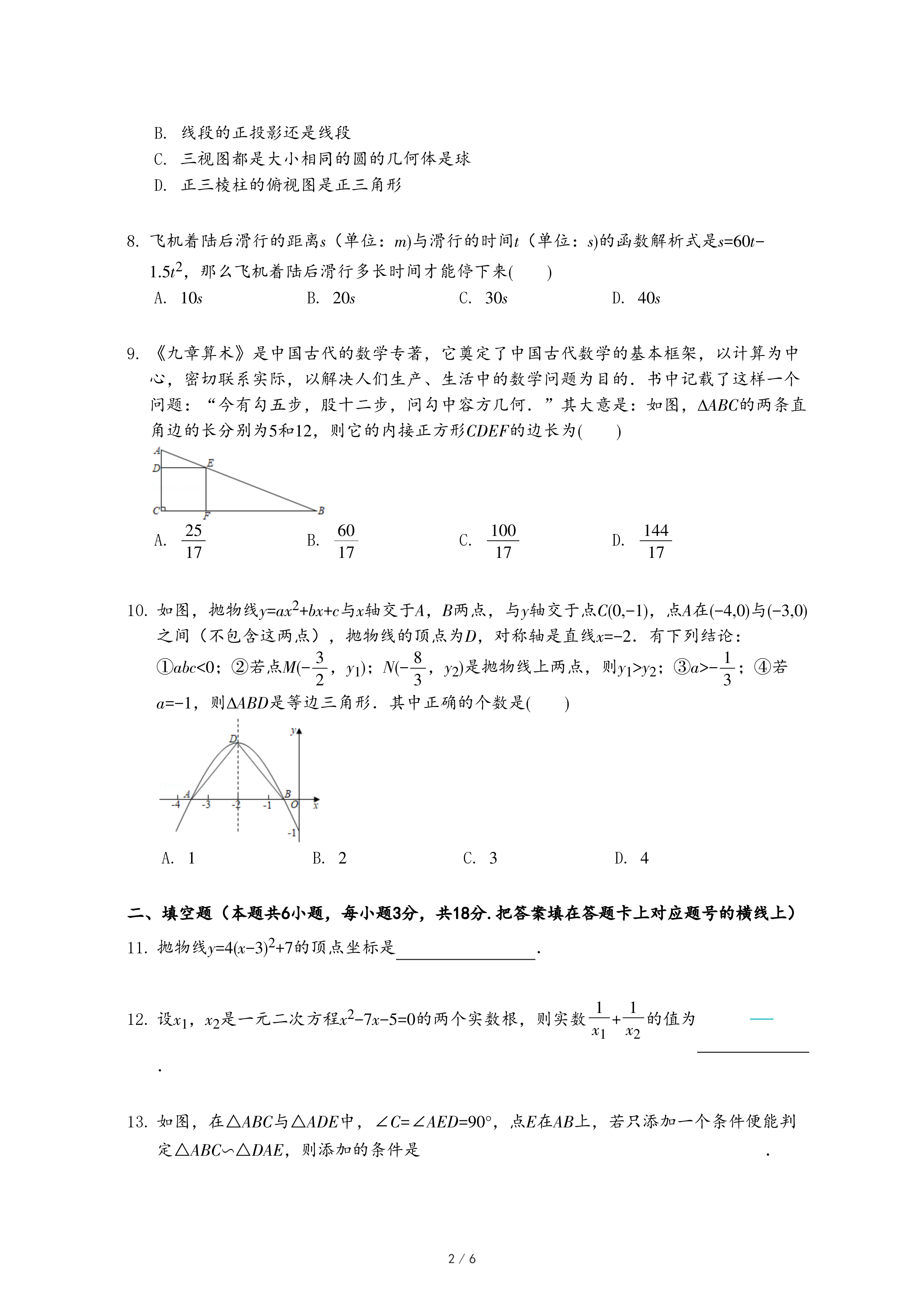
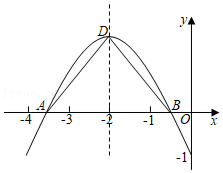
如图2，若∠A=2∠B=60°，b=1，易求得a²-b²的值为      ，bc的值为      ．
（2）【猜想论证】
根据（1）猜想a，b，c之间存在怎样的数量关系？请从下列思路中选择一种证明你的猜想．
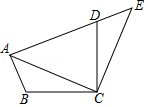
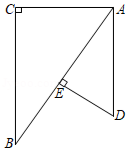
思路一：如图3，延长BA至D，使AD=AC，连接CD．
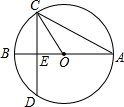
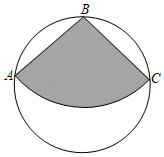
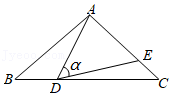
思路二：如图4，作∠BAC的平分线交BC于点D．
（3）【素养提升】
若在这个倍角△ABC中，已知∠A>∠C>∠B，且它的三边长恰好是三个连续的正整数，请根据（2）中的结论直接写出这个三角形的“伴线”长．

24．如图，抛物线y=ax²+4x+c经过A(-3，-4)，B(0，-1)两点，点P是y轴左侧且位于x轴下方抛物线上一动点，设其横坐标为m．
(1)直接写出抛物线的解析式；
(2)将线段AB绕点B顺时针旋转90°得线段BD(点D是点A的对应点)，求点D的坐标，并判断点D是否在抛物线上；
(3)过点P作PM⊥x轴交直线BD于点M，试探究是否存在点P，使△PBM是等腰三角形？若存在，求出点m的值；若不存在，说明理由．