






| 1 |
| a |
| 1 |
| a2 |
| 1 |
| 2 |
| 400 |
| x-30 |
| 500 |
| x |
| 400 |
| x |
| 500 |
| x+30 |
| 400 |
| x |
| 500 |
| x-30 |
| 400 |
| x+30 |
| 500 |
| x |
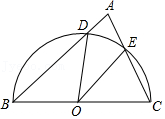
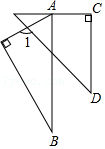
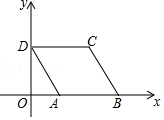
| AC |
| CD |
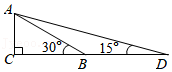
| 1 |
| 2+ √3 |
| 2- √3 |
| (2+ √3 )(2-√3 ) |
| 8 |
| 3 |
| 1 |
√2 |
√2 |
| 2 |
| a2-4 |
| a2-4a+4 |
| 1 |
| 2-a |
| 2 |
| a2-2a |
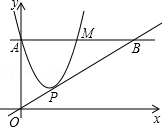
| m |
| x |
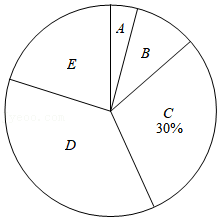
| 分组 | 分数段(分) | 频数 |
| A | 18≤x<22.5 | 2 |
| B | 22.5≤x<27 | 5 |
| C | 27≤x<31.5 | 15 |
| D | 31.5≤x<36 | m |
| E | 36≤x<40.5 | 10 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |