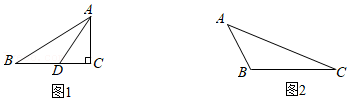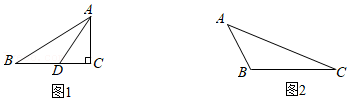17．先化简，再求值：(1-)÷，其中a=2cos60°+()^-1+(π-3)⁰．

18．如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．
(1)求证：△BDE≌△CDF．
(2)当AD⊥BC，AE=2，CF=4时，求AC的长．

19．如图，一次函数y=kx+b的图象与反比例函数y=的图象在第三象限交于点A(-3，-2)，与y轴的正半轴交于点B，且OB=4．
(1)求函数y=和y=kx+b的解析式；
(2)将直线AB向下平移4个单位后得到直线l：y₁=k₁x+b₁(k₁≠0)，l与反比例函数y₂=的图象相交，求使y₁＜y₂成立的x的取值范围．

20．为了解“永远跟党走”主题宣传教育活动的效果，某校组织了党史知识问卷测试，从中抽取部分答卷，统计整理得到不完整的频数分布表和扇形统计图．

根据以上信息，解答下列问题：
(1)填空：m=      ，n=      ，扇形统计图中“D”等级的圆心角为       度；
(2)若成绩不低于90分为优秀，请估计该校2000名学生中达到优秀等级的人数；
(3)已知A等级中有2名男生，现从A等级中随机抽取2名同学，试用列表或树状图的方法求出恰好抽到一男一女的概率．

21．如图，AB，AC切⊙O分别于点B，C，BD∥AC交⊙O于点D，连接CO并延长交BD于点E．
(1)求证：BE=DE；
(2)若⊙O的半径为13，tanA=，求AB的长．

22．某公园有一个截面由抛物线和长方形构成的观景拱桥，如图所示，长方形的长为16米，宽为3米，抛物线的最高处C距地面7米．
(1)经过讨论，同学们得出如图所示的三种建立平面直角坐标系的方案，请从中选择一种求出抛物线的表达式；

(2)观景拱桥下有两根长为4.75米的对称安置的立柱，求这两根立柱的水平距离；
(3)现公园管理处打算，在观景拱桥的下方限高3.5米水平线上，两立柱间安装一个长8米的矩形广告牌EFMN，为安全起见，要求广告牌的最高处与拱桥的桥面之间的距离MH不得小于0.35米，求矩形广告牌的最大高度MF．

23．【阅读理解】
在一个三角形中，如果有两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“亚直角三角形”．根据这个定义，显然α+β＜90°，则这个三角形的第三个角为180°-(α+β)＞90°，这就是说“亚直角三角形”是特殊的钝角三角形．
【尝试运用】
(1)若某三角形是“亚直角三角形”，且一个内角为100°，请直接写出它的两个锐角的度数；
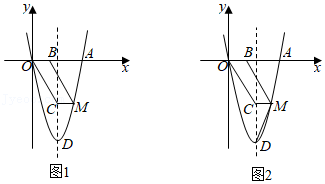
(2)如图1，在Rt△ABC中，∠ACB=90°，AC=6，BC=9，点D在边BC上，连接AD，且AD不平分∠BAC．若△ABD是“亚直角三角形”，求线段AD的长；
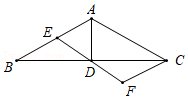
【素养提升】
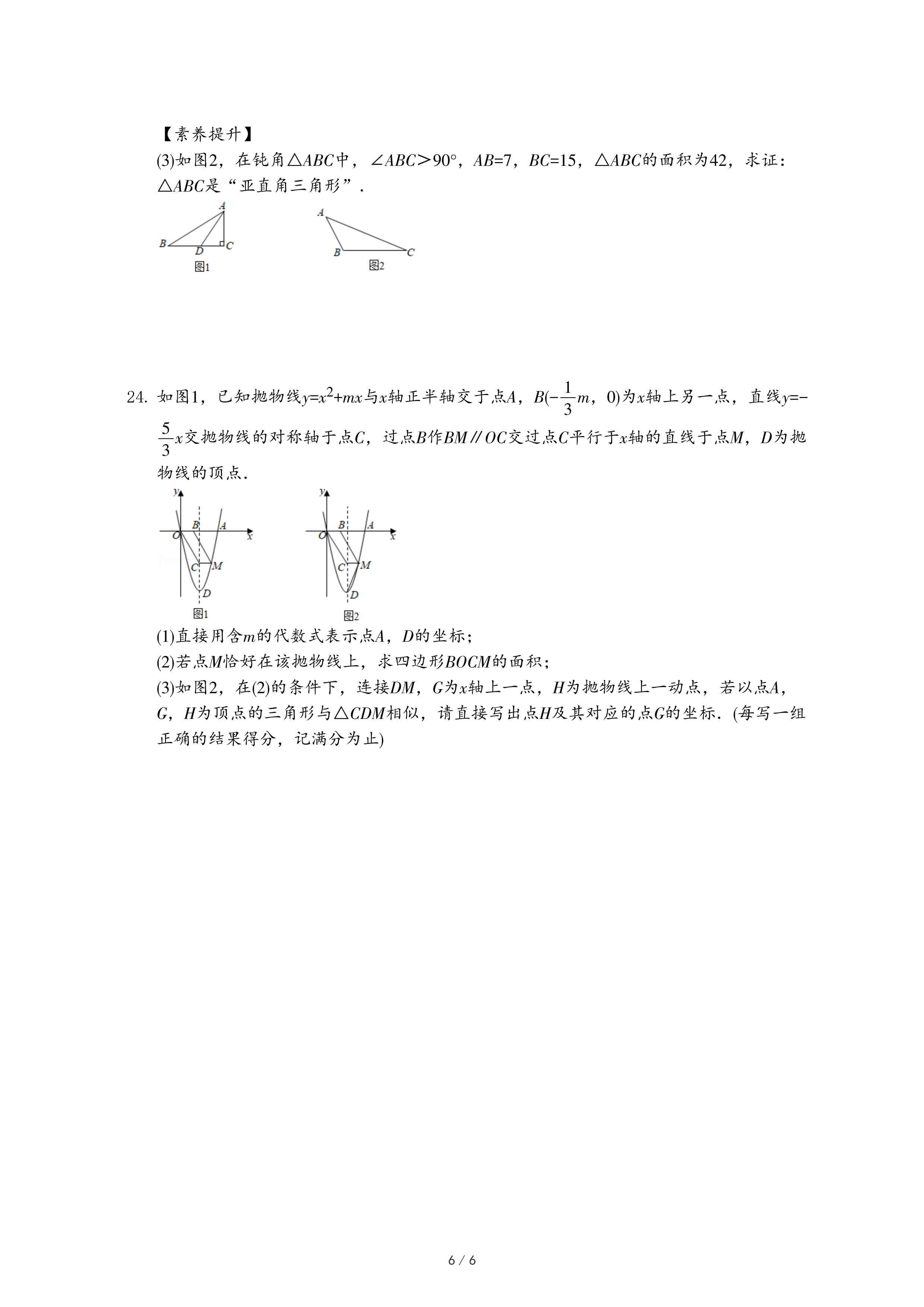
(3)如图2，在钝角△ABC中，∠ABC＞90°，AB=7，BC=15，△ABC的面积为42，求证：△ABC是“亚直角三角形”．

24．如图1，已知抛物线y=x²+mx与x轴正半轴交于点A，B(-m，0)为x轴上另一点，直线y=-x交抛物线的对称轴于点C，过点B作BM∥OC交过点C平行于x轴的直线于点M，D为抛物线的顶点．

(1)直接用含m的代数式表示点A，D的坐标；
(2)若点M恰好在该抛物线上，求四边形BOCM的面积；
(3)如图2，在(2)的条件下，连接DM，G为x轴上一点，H为抛物线上一动点，若以点A，G，H为顶点的三角形与△CDM相似，请直接写出点H及其对应的点G的坐标．(每写一组正确的结果得分，记满分为止)