17．计算：(-)^-2-(π-3.14)⁰-|-2|+sin60°．

18．先化简，再求值：÷-，其中x=．

19．一艘船向正北方向航行，在A处时看到灯塔S在船的北偏东30°的方向上，继续航行12海里到达B处，看到灯塔S在船的北偏东60°的方向上，若继续沿正北方向航行，求航行过程中船距灯塔S的最近距离．(结果精确到0.1海里)(参考数据：≈1.41，≈1.73)

20．某校为了了解初中学生每天的睡眠时间(单位为小时)，随机调查了该校的部分初中学生，根据调查结果，绘制出如图统计图．

请根据相关信息，解答下列问题：
(1)本次接受调查的初中学生人数为      人，扇形统计图中的m=      ，条形统计图中的n=      ；
(2)所调查的初中学生每天睡眠时间的众数是      ，方差是      ；
(3)该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．

21．如图1，ABCD是平行四边形对角线AC，BD相交于点O，直线EF过点O，分别交AD，BC于点E，F．
(1)求证：AE=CF．
(2)如图2，若ABCD是老张家的一块平行四边形田地．P为水井，现要把这块田地平均分给两个儿子，为了用水方便，要求分给两个儿子的田地都与水井P相邻．请你帮老张家设计一下．画出图形，并说明理由？

22．已知某酒店的三人间和双人间客房标价为：三人间和双人间每天都是600元，为吸引客源，促进旅游，在“十•一”黄金周期间酒店进行优惠大酬宾，凡团体入住一律五折优惠．一个50人的旅游团在十月二号到该酒店住宿，租住了一些三人间、双人间客房，要求租住的房间正好被住满．
(1)如果一天一共花去住宿费6300元．求租住了三人间、双人间客房各多少间？
(2)设三人间共住了x人，这个团一天一共花去住宿费y元，请写出y与x的函数关系式；
(3)一天6300元的住宿费是否为最低？如果不是，请设计一种方案，并使住宿费用最低，请写出设计方案，并求出最低的费用．

23．如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，将△ABC沿直线AB折叠得到△ABD，交⊙O于点D．连接CD交AB于点E，延长BD和CA相交于点P，过点A作AG∥CD交BP于点G．
(1)求证：直线GA是⊙O的切线；
(2)求证：AC²=GD•BD；
(3)若tan∠AGB=，PG=6，求cos∠P的值．

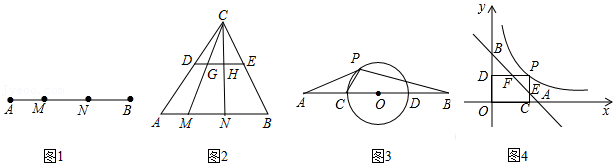
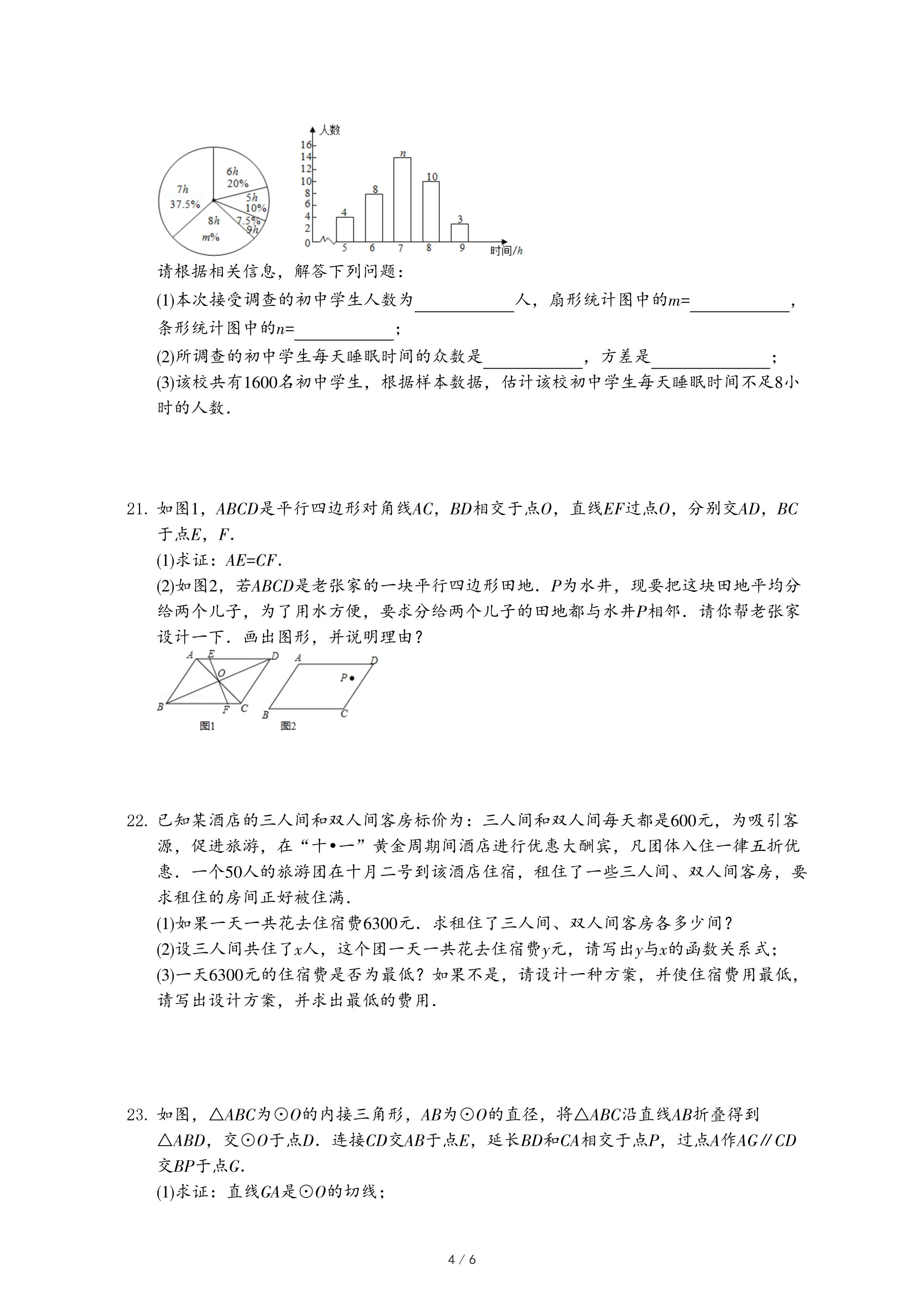
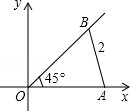
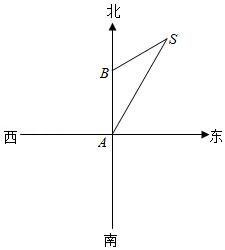
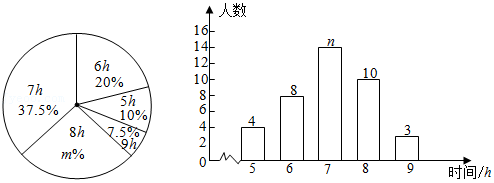
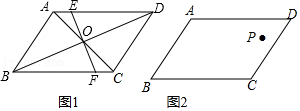
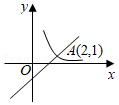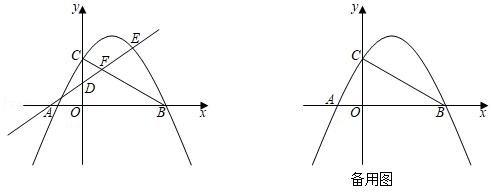24．(1)定义：如图1，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股点．已知点M、N是线段AB的勾股点，若AM=1，MN=2，则BN=      ．
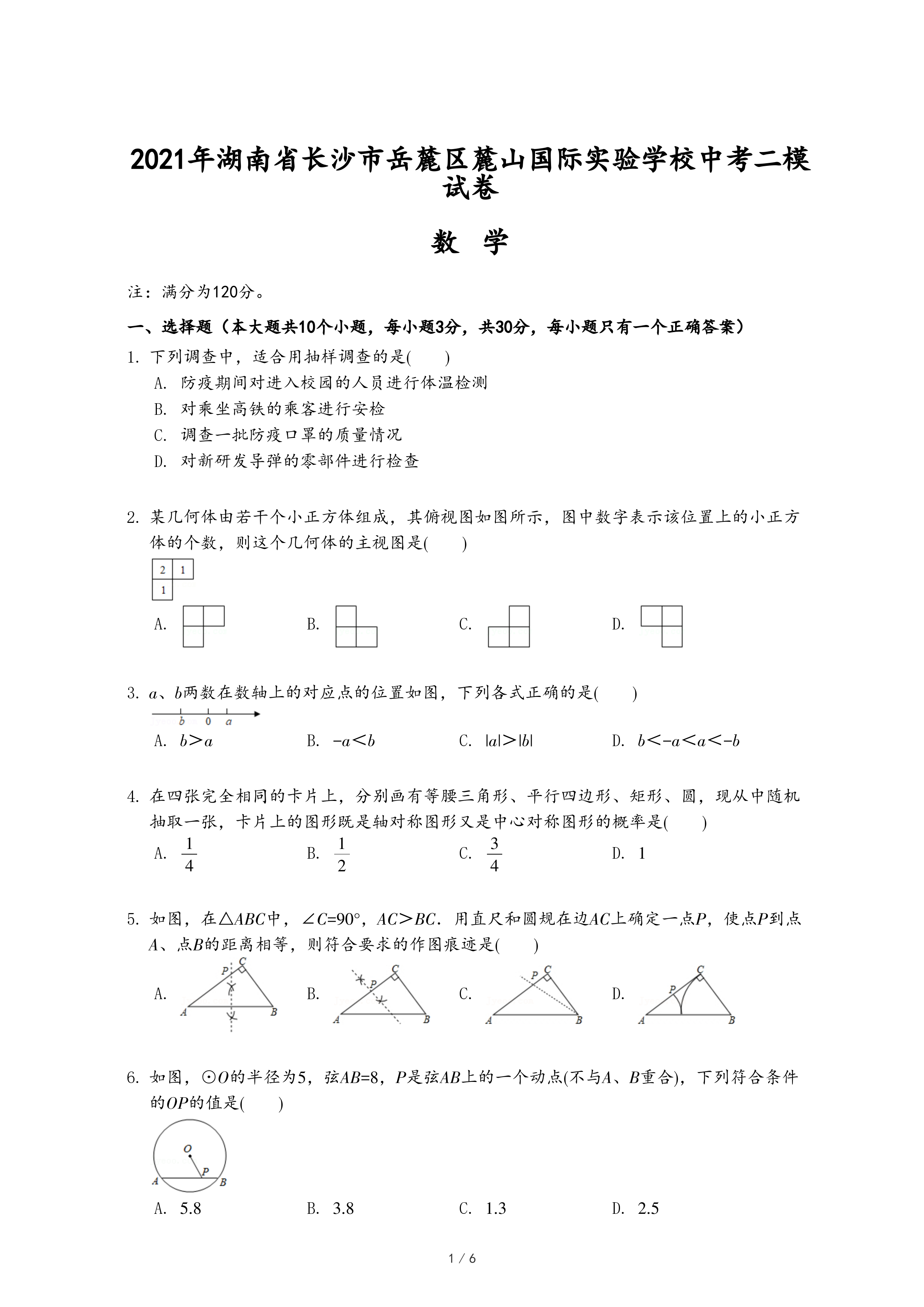
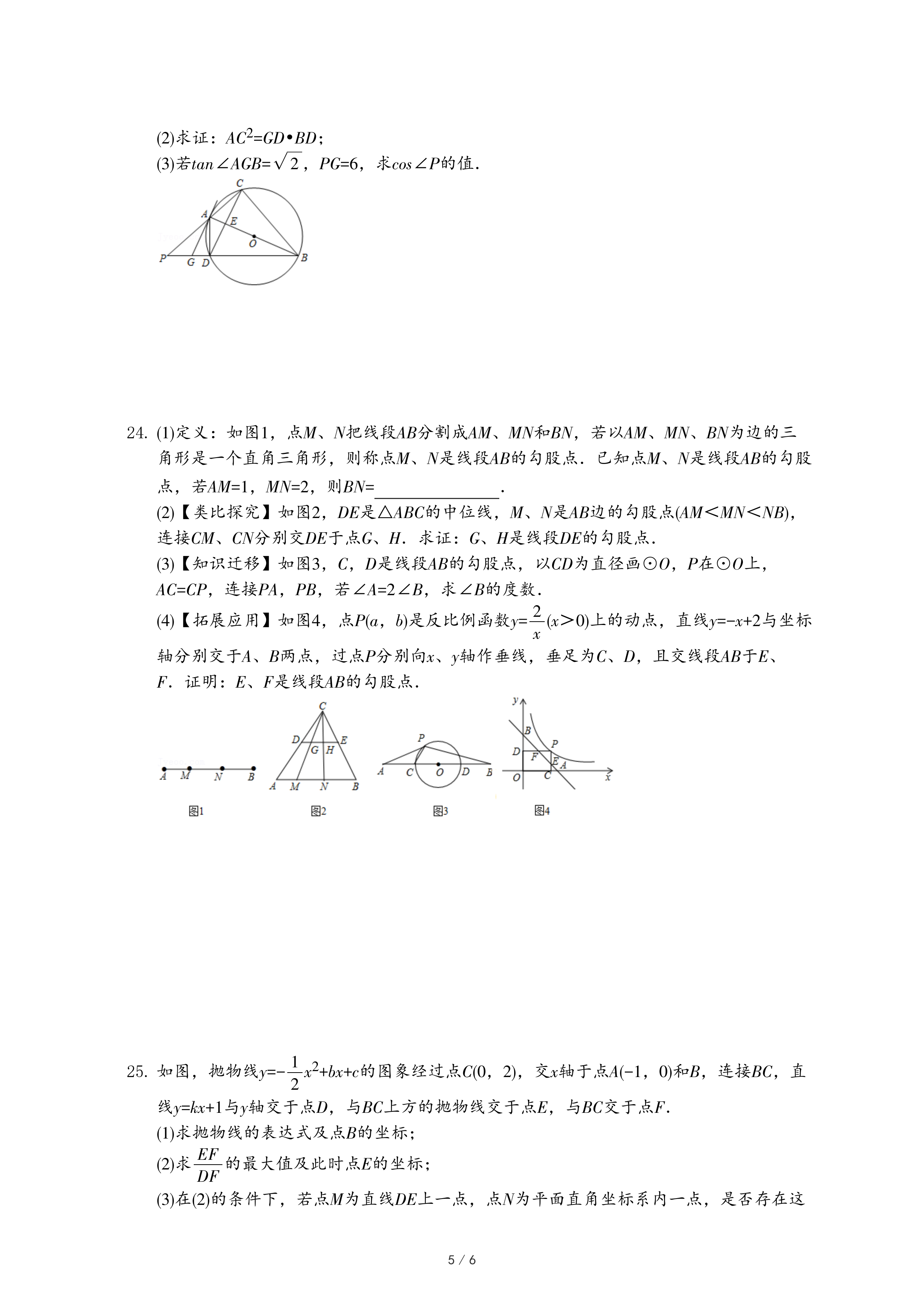
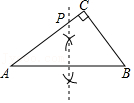
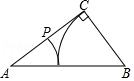
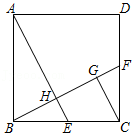
(2)【类比探究】如图2，DE是△ABC的中位线，M、N是AB边的勾股点(AM＜MN＜NB)，连接CM、CN分别交DE于点G、H．求证：G、H是线段DE的勾股点．
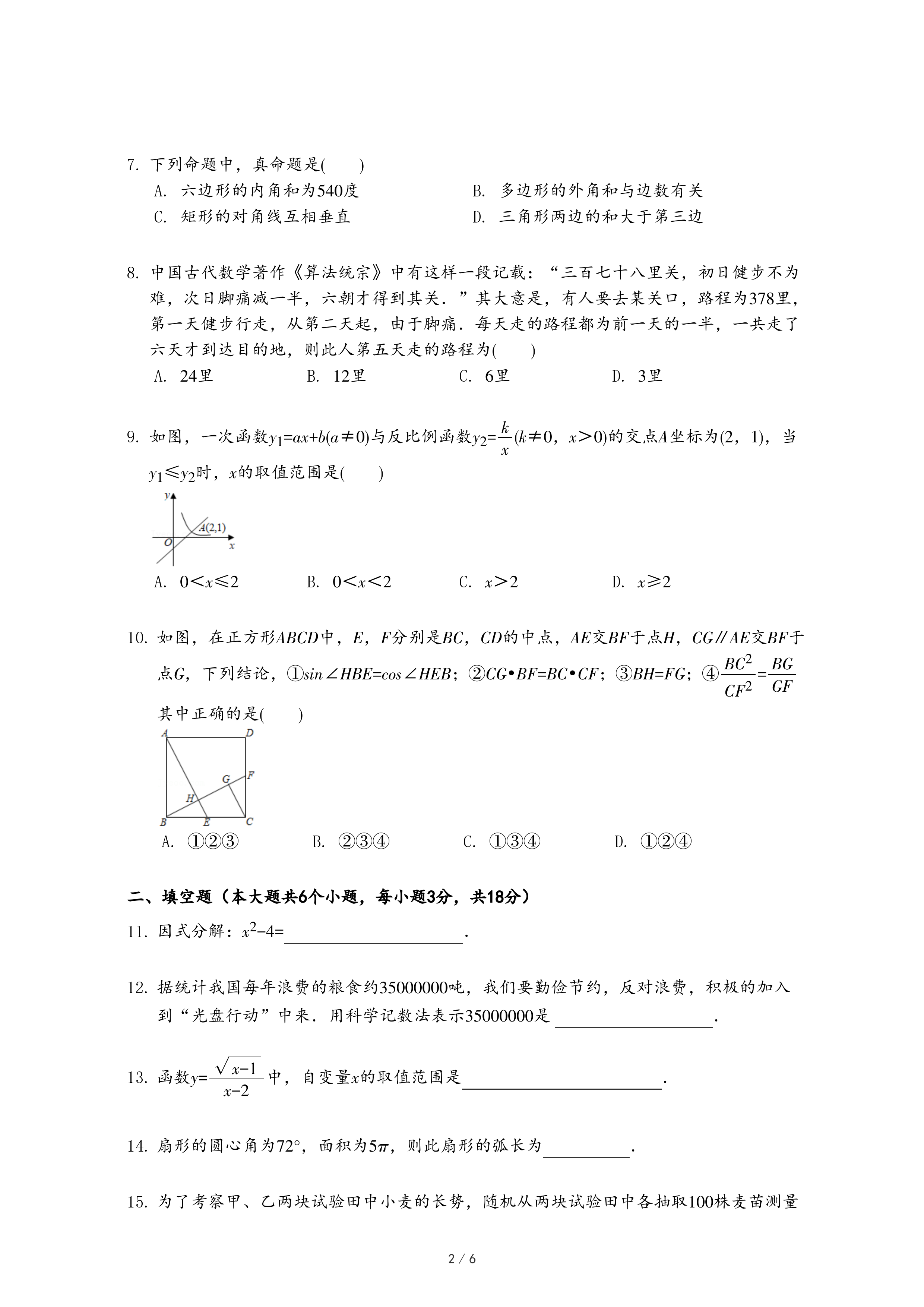
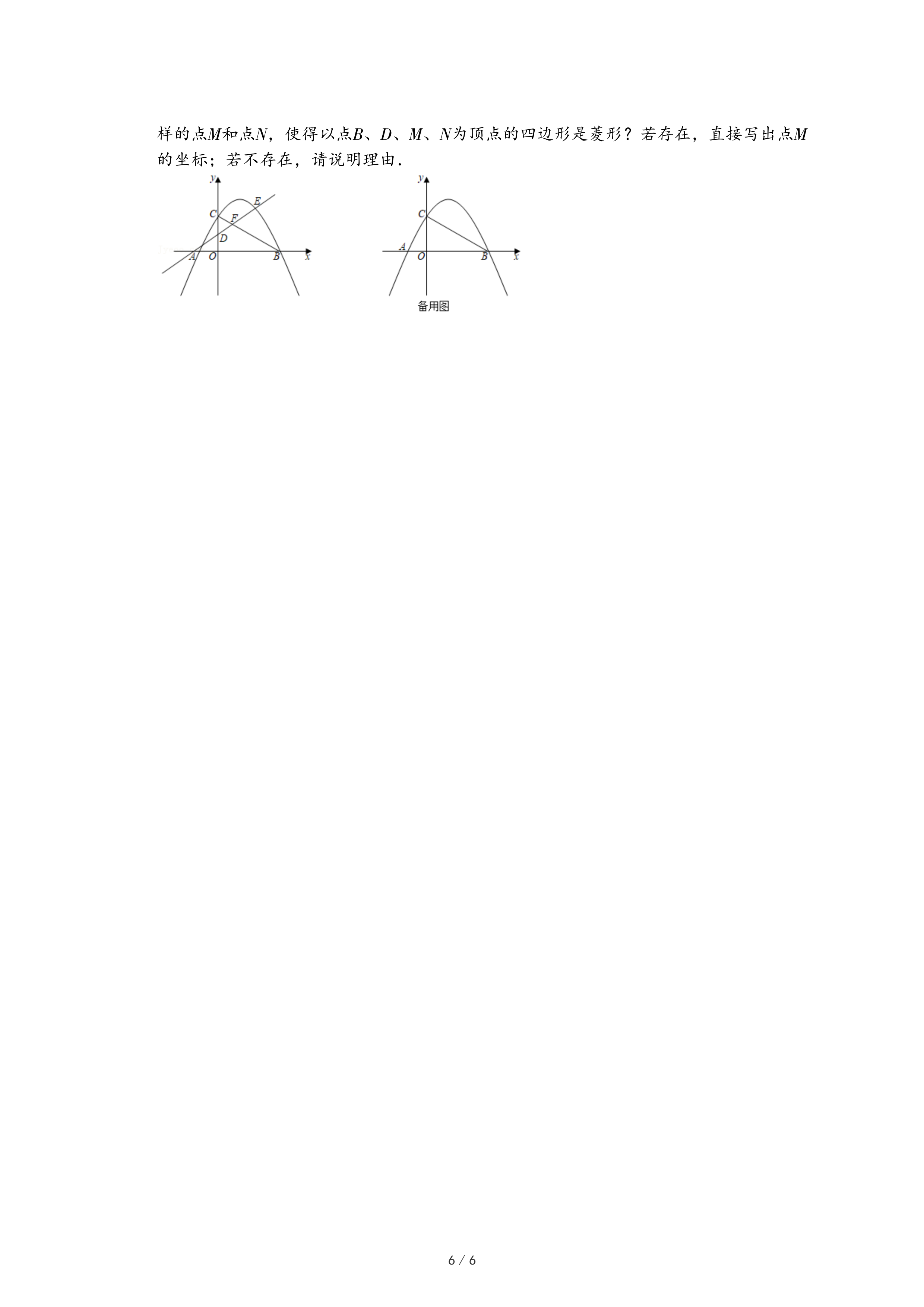
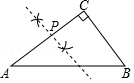
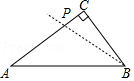
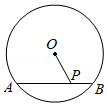
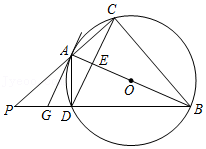
(3)【知识迁移】如图3，C，D是线段AB的勾股点，以CD为直径画⊙O，P在⊙O上，AC=CP，连接PA，PB，若∠A=2∠B，求∠B的度数．
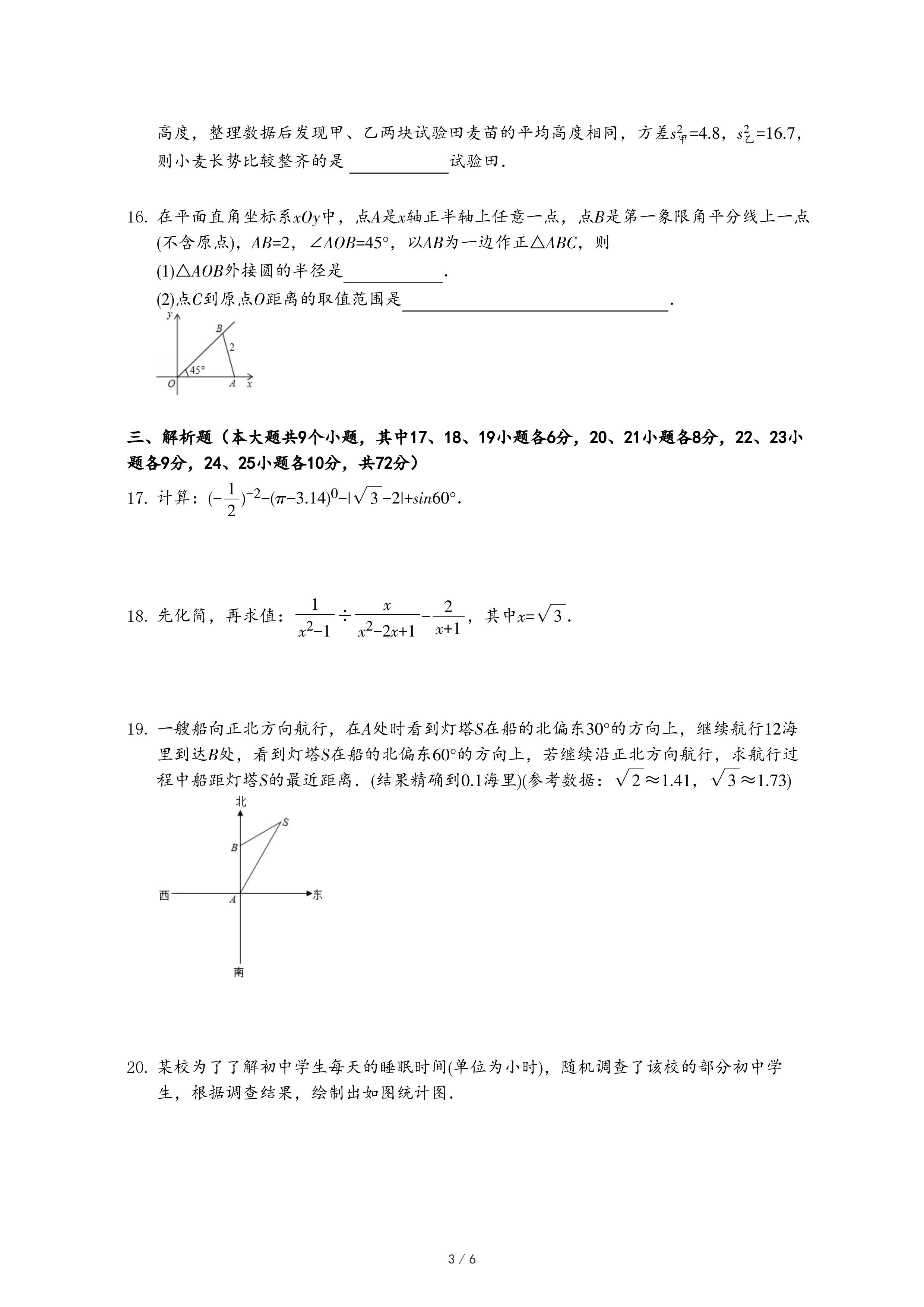
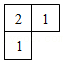
(4)【拓展应用】如图4，点P(a，b)是反比例函数y=(x＞0)上的动点，直线y=-x+2与坐标轴分别交于A、B两点，过点P分别向x、y轴作垂线，垂足为C、D，且交线段AB于E、F．证明：E、F是线段AB的勾股点．

25．如图，抛物线y=-x²+bx+c的图象经过点C(0，2)，交x轴于点A(-1，0)和B，连接BC，直线y=kx+1与y轴交于点D，与BC上方的抛物线交于点E，与BC交于点F．
(1)求抛物线的表达式及点B的坐标；
(2)求的最大值及此时点E的坐标；
(3)在(2)的条件下，若点M为直线DE上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B、D、M、N为顶点的四边形是菱形？若存在，直接写出点M的坐标；若不存在，请说明理由．