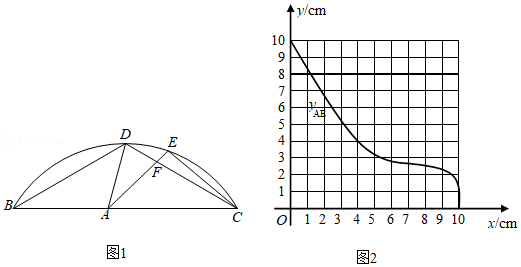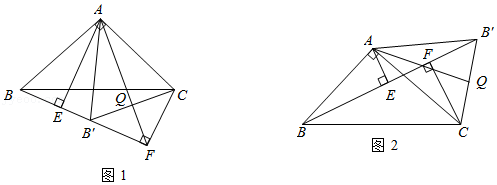



| 1 |
| 2021 |
| 1 |
| 2021 |
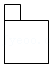
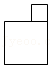

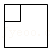
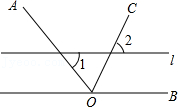
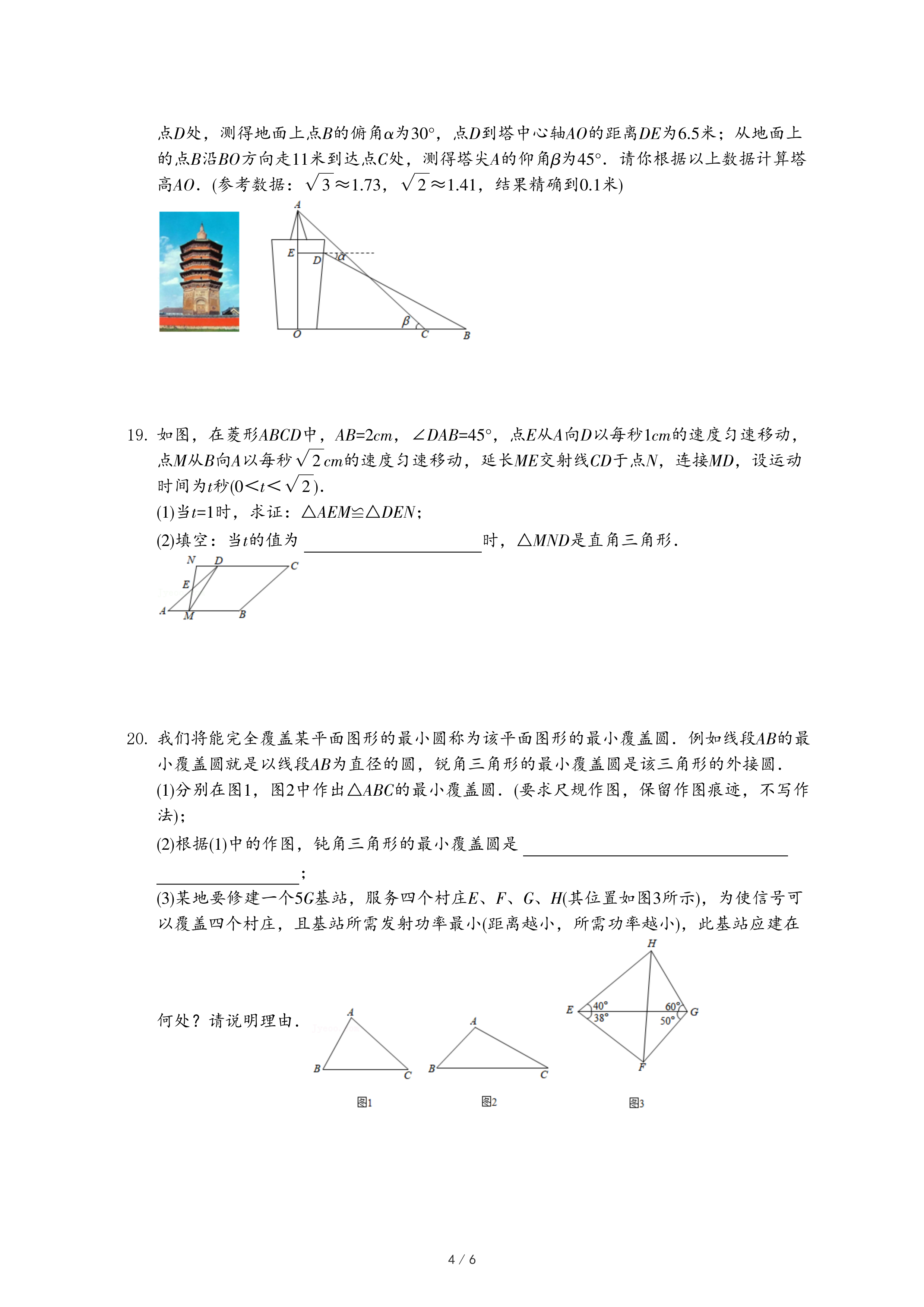
| 1 |
| 20000 |
| 1 |
| 20000 |
| k |
| x |
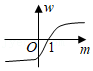
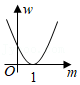
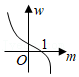
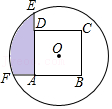
| x2-y2 |
| x |
| 2xy-y2 |
| x |
| 1 |
| x |
| 1 |
| y |
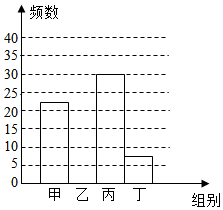
| 组别 | 分数段 | 频数 | 频率 |
| 甲 | 90≤x≤100 | 22 | 0.22 |
| 乙 | 80≤x<90 | a | 0.4 |
| 丙 | 70≤x<80 | 30 | b |
| 丁 | 60≤x<70 | 8 | 0.08 |
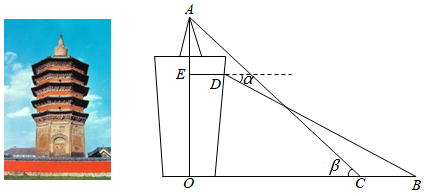
| AB/cm | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| AC/cm | 10.0 | 9.0 | 8.0 | 7.0 | 6.0 | 5.0 | 4.0 | 3.0 | 2.0 | 1.0 | 0 |
| AE/cm | 10.0 | 8.4 | 6.8 | 5.2 | 3.9 | 3.1 | 2.7 | 2.6 | 2.5 | 2.2 | 0 |
| EC/cm | 0 | 1.1 | 2.2 | 3.2 | 4.0 | 4.4 | 4.4 | 4.1 | 3.6 | 2.7 | 0 |