15．解不等式组：，并把解集在数轴上表示出来．

16．观察下列两个等式：1-=2×1×-1，2-=2×2×-1给出定义如下：我们称使等式a-b=2ab-1成立的一对有理数a、b为“同心有理数对”，记为(a，b)，如：数对(1，)，(2，)，都是“同心有理数对”．
(1)数对(-2，1)，(3，)是“同心有理数对”的是      ．
(2)若(a，3)是“同心有理数对”，求a的值；
(3)若(m，n)是“同心有理数对”，则(-n，-m)      “同心有理数对”(填“是”或“不是”)，说明理由．

17．平面直角坐标系中，点A的坐标是(0，3)，点B在x轴上，将△AOB绕点A逆时针旋转90°得到△ACD，点O、B对应点分别是C、D．
(1)若点B的坐标是(-4，0)，请在图中画出△ACD，并写出点C、D的坐标；
(2)当点D落在第一象限时，试写出一个符合条件的点B的坐标．

18．如图，一次“台风”过后，一根旗杆被台风从高地面5米处吹断，倒下的旗杆的顶端落在离旗杆底部12米处，那么这根旗杆被吹断裂前至少有多高？

19．第一盒中有2个白球、1个红球，第二盒中有1个白球、1个红球，这些球除颜色外无其他差别，分别从每个盒中随机取出1个球．
(1)在第一盒中取出1个球是白球的概率是    ；
(2)求取出的2个球中1个白球、1个红球的概率．

20．问题提出
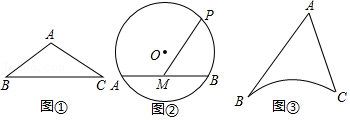
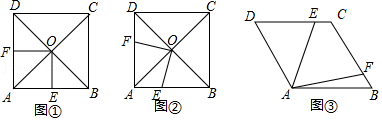
(1)如图①，在△ABC中，∠A=120°，AB=AC=5，则△ABC的外接圆半径R的值为      ．
问题探究
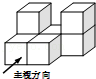
(2)如图②，⊙O的半径为13，弦AB=24，M是AB的中点，P是⊙O上一动点，求PM的最大值．
问题解决
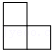
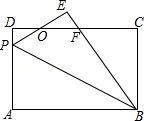
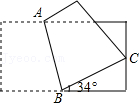
(3)如图③所示，AB、AC、⌒BC是某新区的三条规划路，其中AB=6km，AC=3km，∠BAC=60°，⌒BC所对的圆心角为60°，新区管委会想在⌒BC路边建物资总站点P，在AB，AC路边分别建物资分站点E、F，也就是，分别在⌒BC、线段AB和AC上选取点P、E、F．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷、环保和节约成本．要使得线段PE、EF、FP之和最短，试求PE+EF+FP的最小值．(各物资站点与所在道路之间的距离、路宽均忽略不计)

21．某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品，售后经过统计得到此商品单价在第x天(x为正整数)销售的相关信息，如表所示：

(1)第      天该商品单价为25元/件？
(2)求销售该商品30天里所获利润y(元)关于x(天)的函数关系式；
(3)这30天中第几天获得的利润最大？最大利润是多少？

22．为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系．
(1)求y与x的函数关系式；
(2)若在购买计划中，B种苗的数量不少于22棵但不超过35棵，请设计购买方案，使总费用最低，并求出最低费用．

23．问题原型：如图①，正方形ABCD的对角线交于点O，点E、F分别为边AB、AD中点，且∠EOF=90°，易得四边形AEOF的面积是正方形ABCD的面积的四分之一．(不用证明)

(1)探究发现：某数学兴趣小组，尝试改变点E、F的位置，点E、F分别为边AB、AD上任一点，且∠EOF=90°，如图②，探究：四边形AEOF的面积是否为正方形ABCD面积的四分之一？并说明理由．
(2)拓展提升：如图③，菱形ABCD中，∠BAD=120°，∠EAF=60°，且点E、F分别在边DC、BC上，四边形AECF的面积是菱形ABCD面积的几分之一？(直接写出结果即可)