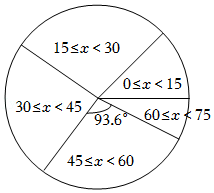



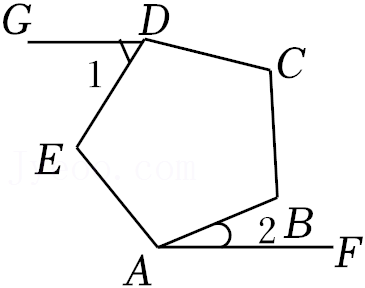
| 1 |
| 7 |
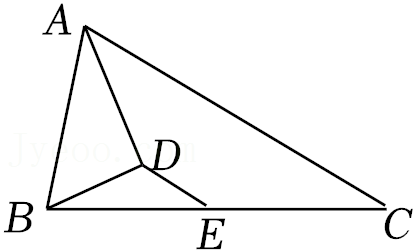
| 1 |
| 2 |
| 3 |
| 2 |
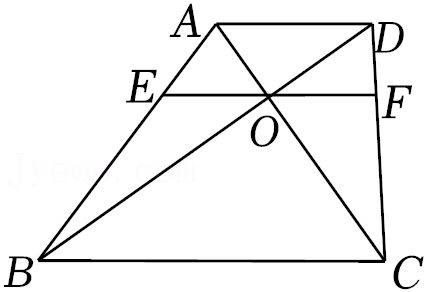
| AE |
| BE |
| DF |
| CF |
| 1 |
| AD |
| 1 |
| BC |
| 1 |
| OE |
| 1 |
| AD |
| 1 |
| BC |
| 1 |
| OF |
| AD |
| EF |
| EF |
| BC |
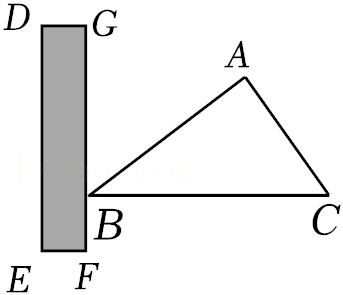
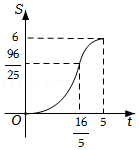
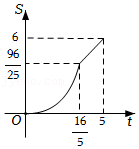
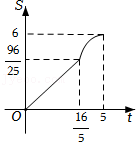
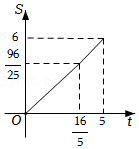
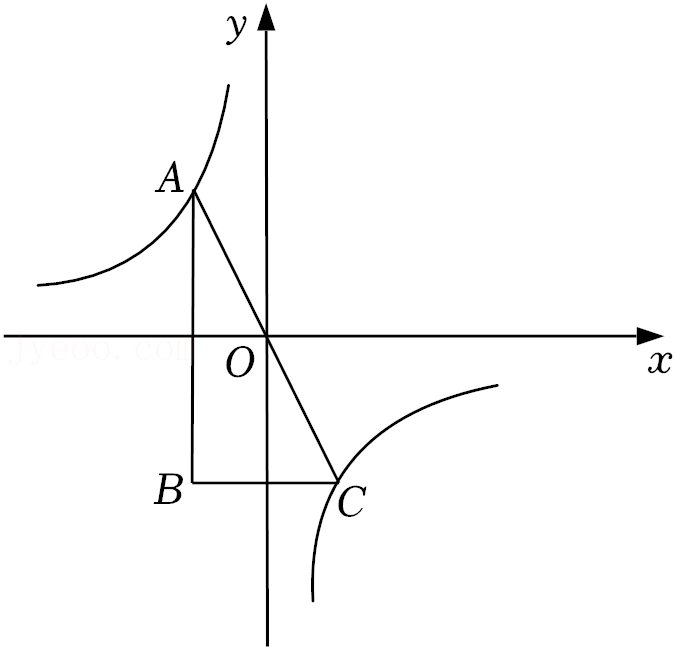
| k |
| x |
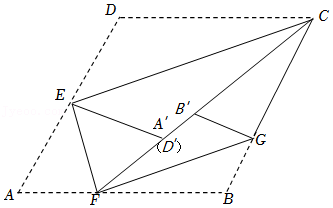
| FG |
| CE |
| 3 |
| 4 |
| 1 |
| 1×2 |
| 1-2 |
| 1+1 |
| 1 |
| 2×3 |
| 4-2 |
| 4+2 |
| 1 |
| 2 |
| 1 |
| 3×4 |
| 9-2 |
| 9+3 |
| 1 |
| 3 |
| 1 |
| 4×5 |
| 16-2 |
| 16+4 |
| 1 |
| 4 |
| 1 |
| 5×6 |
| 25-2 |
| 25+5 |
| 1 |
| 5 |
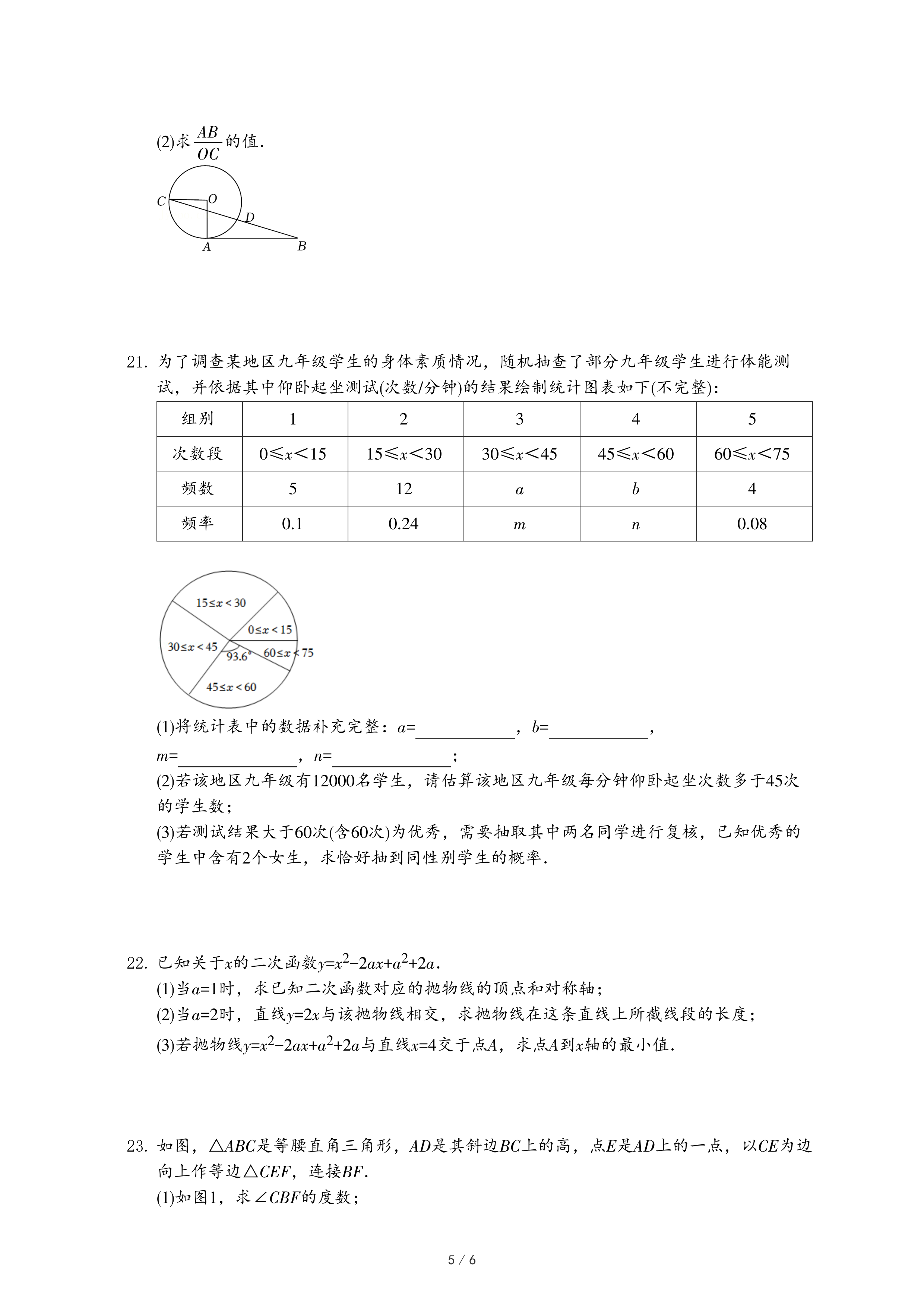
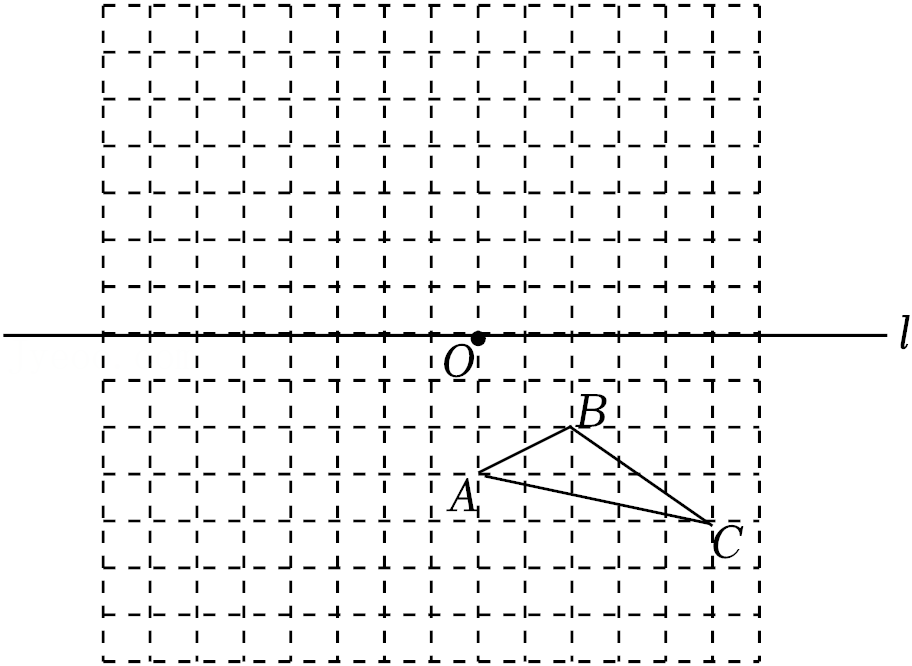
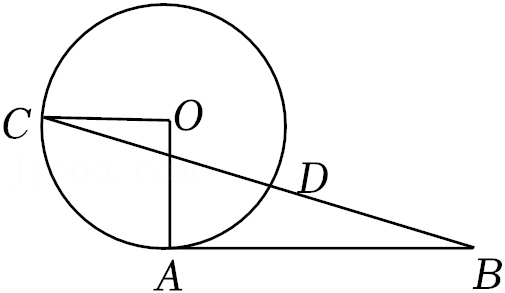
| AB |
| OC |
| 组别 | 1 | 2 | 3 | 4 | 5 |
| 次数段 | 0≤x<15 | 15≤x<30 | 30≤x<45 | 45≤x<60 | 60≤x<75 |
| 频数 | 5 | 12 | a | b | 4 |
| 频率 | 0.1 | 0.24 | m | n | 0.08 |