25.自从开展“创建全国文明城区”工作以来,门头沟区便掀起了“门头沟热心人”志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
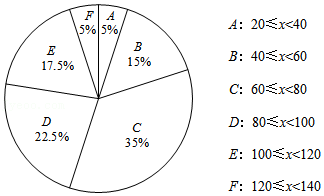
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成5组:20≤x<40,40≤x<60,60≤x<80,80≤x<100,100≤x<120,120≤x<140):
b.甲校40名学生一周志愿服务时长在60≤x<80这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
| 学校 | 平均数 | 中位数 | 众数 |
| 甲校 | 75 | m | 90 |
| 乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)m=
;
(2)根据上面的统计结果,你认为①
所学校学生志愿服务工作做得好(填“甲”或“乙”),理由②
;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有
人.