首页 > 初中试卷 > 九年级试卷 > 九年级数学试卷 > 2020年九年级数学试卷 > 2020年北京九年级数学试卷 > 2020年北京房山区九年级数学试卷 > 2020年北京房山区数学中考模拟试卷

2020年北京市房山区中考数学二模试卷

试卷格式：2020年北京市房山区中考数学二模试卷.PDF
试卷热词：最新试卷、2020年、北京试卷、房山区试卷、数学试卷、九年级试卷、中考模拟试卷、初中试卷
如何查看答案以及解析
下载试卷后，用微信扫一扫扫描试卷右上角二维码即可查看【2020年北京市房山区中考数学二模试卷】解析和视频讲解。
试卷题目
1．在迎来庆祝新中国成立70周年之后，对于中国而言，2020年又将是一个新的时间坐标．过去40年，中国完成了卓越的经济转型，八亿两千万人成功脱贫，这是人类发展史上具有里程碑意义的重大成就．将820000000用科学记数法表示为(　　)
  • A. 8.2×109
  • B. 0.82×109
  • C. 8.2×108
  • D. 82×107
2．如图是某个几何体的三视图，该几何体是(　　)

  • A. 长方体
  • B. 三棱柱
  • C. 正方体
  • D. 圆柱
3．实数a，b在数轴上的对应点的位置如图所示，则正确的结论是( )

  • A. |b|＜a
  • B. -a＜b
  • C. a+b＞0
  • D. |a|＞b
4．《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求，于2020年5月1日起施行，施行的目的在于加强生活垃圾管理，改善城乡环境，保障人体健康．下列垃圾分类标志，是中心对称图形的是(　　)
  • A.
  • B.
  • C.
  • D.
5．李老师是一位运动达人，他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数，并绘制成如图统计表，在每天所走的步数这组数据中，众数和中位数分别是(　　)

  • A. 1.6，1.5
  • B. 1.7，1.6
  • C. 1.7，1.7
  • D. 1.7，1.55
6．如图，在▱ABCD中，延长AD至点E，使AD=2DE，连接BE交CD于点F，交AC于点G，则
CG
AG
的值是(　　)

  • A.
    2
    3
  • B.
    1
    3
  • C.
    1
    2
  • D.
    3
    4

7．如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

下面有三个推断：
①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；
②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；
③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．
其中合理的是(　　)
  • A. ①
  • B. ②
  • C. ①②
  • D. ①③
8．2020年是5G爆发元年，三大运营商都在政策的支持下，加快着5G建设的步伐．某通信公司实行的5G畅想套餐，部分套餐资费标准如下：
套餐类型 月费(元/月) 套餐内包含内容 套餐外资费 
国内数据流量(GB) 国内主叫(分钟) 国内流量 国内主叫 
套餐1 128 30 200 每5元1GB，用满3GB后每3元1GB，不足部分按照0.03元/MB收取 0.19元/分钟 
套餐2 158 40 300 
套餐3 198 60 500 
套餐4 238 80 600 

小武每月大约使用国内数据流量49GB，国内主叫350分钟，若想使每月付费最少，则他应预定的套餐是(　　)
  • A. 套餐1
  • B. 套餐2
  • C. 套餐3
  • D. 套餐4
9．若分式
x+1
x-1
的值为0，则x的值是      ．
10．如图，扇形AOB，通过测量、计算，得⌒AB的长约为      cm．(π取3.14，结果保留一位小数)
11．如图，若在象棋棋盘上建立直角坐标系，使“帅”位于点(-3，-2)，“炮”位于点(-2，0)，则“兵”位于的点的坐标为      ．

12．如图，一个正方形被分成两个正方形和两个一模一样的矩形，请根据图形，写出一个含有a，b的正确的等式      ．

13．如果m+n=4，那么代数式(
m2+n2
m
+2n)•
2m
m+n
的值为      ．
14．已知一组数据x1，x2，x3，…，xn的方差是S2，那么另一组数据x1-3，x2-3，x3-3，…，xn-3的方差是      ．
15．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中记载了一个“折竹抵地”问题：“今有竹高二丈，末折抵地，去本六尺，问折者高几何？”
译文：“有一根竹子，原高二丈(1丈=10尺)，现被风折断，竹梢触地面处与竹根的距离为6尺，问折断处离地面的高度为多少尺？”
如图，我们用点A，B，C分别表示竹梢，竹根和折断处，设折断处离地面的高度BC=x尺，则可列方程为      ．

16．下面是“作一个30°角”的尺规作图过程．
已知：平面内一点A．
求作：∠A，使得∠A=30°．
作法：如图，
(1)作射线AB；
(2)在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；
(3)以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD．
∠DAB即为所求的角．
请回答：该尺规作图的依据是      ．

17．计算：
√18
-(
1
5
)-1+4sin30°+|
√2
-1|．
18．解不等式组：．
19．如图，在△ABC中，BD平分∠ABC交AC于点D，DE∥AB交BC于点E，F是BD中点．求证：EF平分∠BED．

20．已知关于x的一元二次方程kx2-4x+3=0．
(1)当k=1时，求此方程的根；
(2)若此方程有两个不相等的实数根，求k的取值范围．
21．如图，菱形ABCD中，分别延长DC，BC至点E，F，使CE=CD，CF=CB，连接DB，BE，EF，FD．
(1)求证：四边形DBEF是矩形；
(2)若AB=5，cos∠ABD=
3
5
，求DF的长．

22．在平面直角坐标系xOy中，反比例函数y=
k
x
(x＞0)的图象与直线y=x-1交于点A(3，m)．
(1)求k的值；
(2)已知点P(n，0)(n＞0)，过点P作垂直于x轴的直线，交直线y=x-1于点B，交函数y=
k
x
(x＞0)于点C．
①当n=4时，判断线段PC与BC的数量关系，并说明理由；
②若PC≤BC，结合图象，直接写出n的取值范围．

23．如图，在△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，E是AC中点，连接DE．
(1)判断DE与⊙O的位置关系并说明理由；
(2)设CD与OE的交点为F，若AB=10，BC=6，求OF的长．

24．GDP是指一个国家(或地区)在一定时期内生产活动的最终成果，常被公认为是衡量经济状况的最佳指标．截止2020年4月27日，对除西藏外的30个省区市第一季度有关GDP的数据进行收集、整理、描述和分析．下面给出了部分信息：
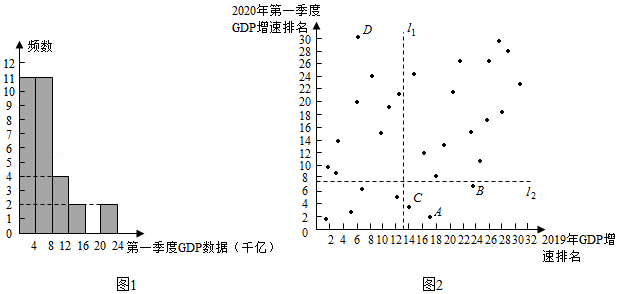
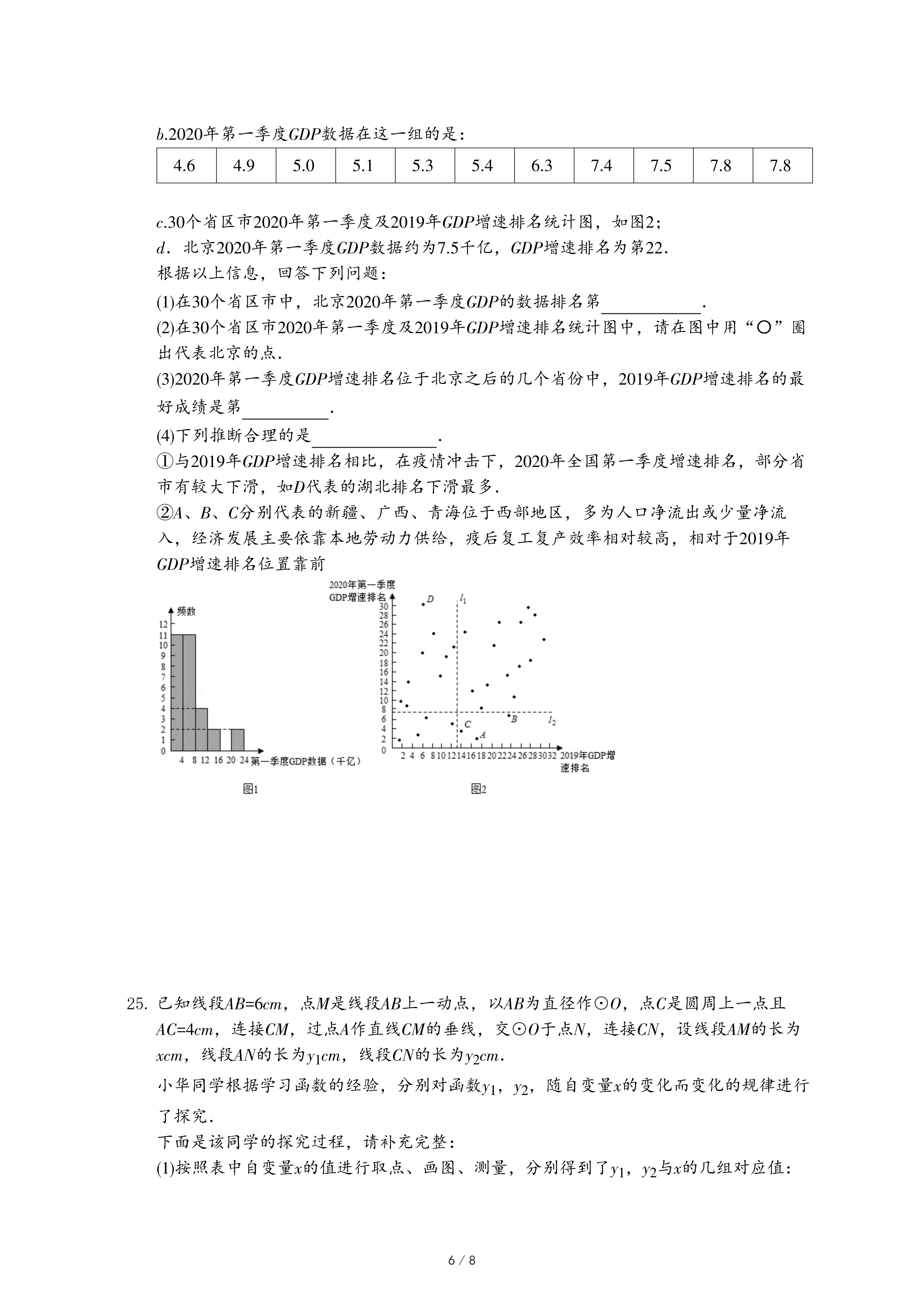
a．各省区市GDP数据的频数分布直方图，如图1(数据分成6组，各组是0＜x≤4，4＜x≤8，8＜x≤12，12＜x≤16，16＜x≤20，20＜x≤24)；
b.2020年第一季度GDP数据在这一组的是：
4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8 

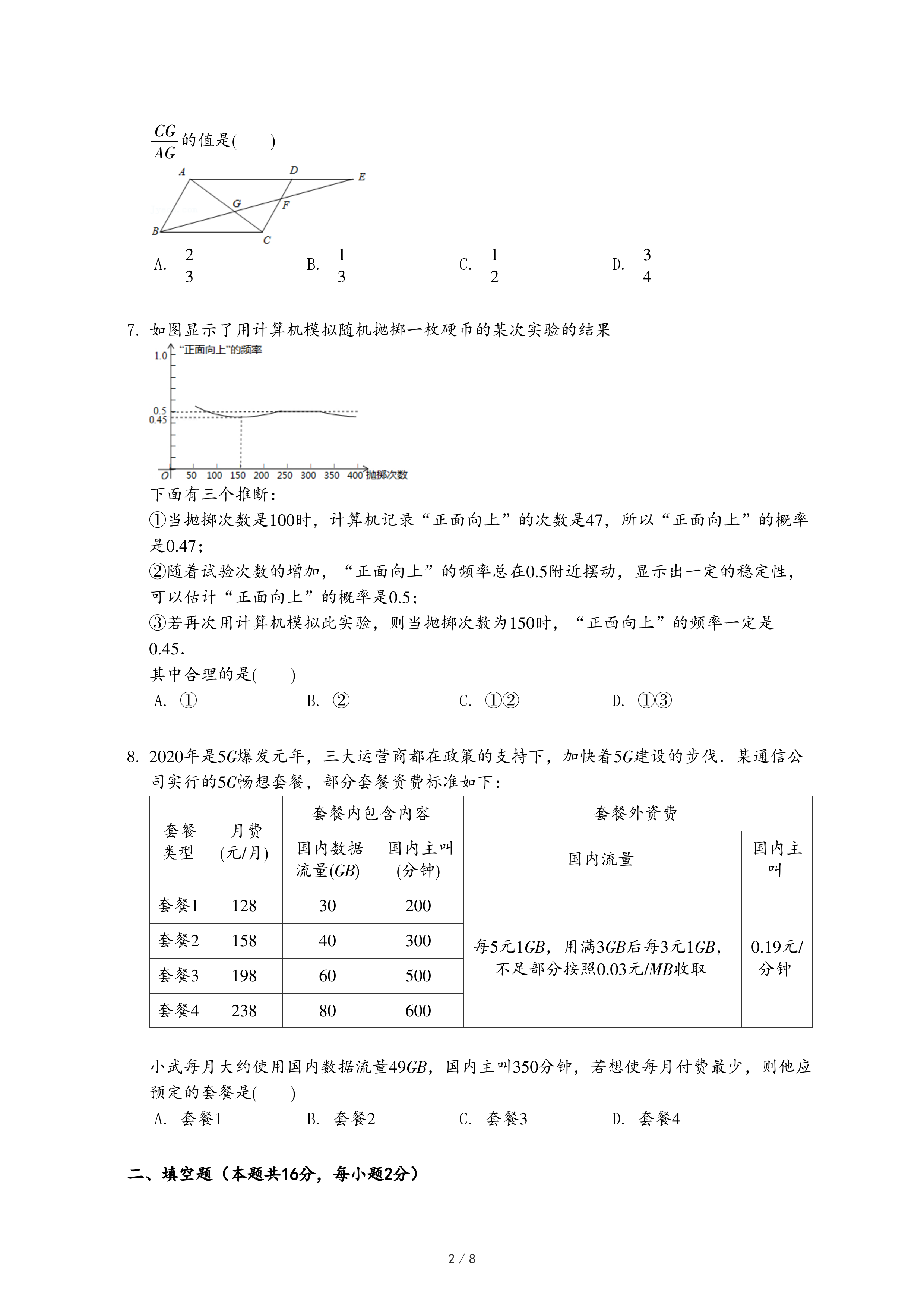
c.30个省区市2020年第一季度及2019年GDP增速排名统计图，如图2；
d．北京2020年第一季度GDP数据约为7.5千亿，GDP增速排名为第22．
根据以上信息，回答下列问题：
(1)在30个省区市中，北京2020年第一季度GDP的数据排名第      ．
(2)在30个省区市2020年第一季度及2019年GDP增速排名统计图中，请在图中用“〇”圈出代表北京的点．
(3)2020年第一季度GDP增速排名位于北京之后的几个省份中，2019年GDP增速排名的最好成绩是第      ．
(4)下列推断合理的是      ．
①与2019年GDP增速排名相比，在疫情冲击下，2020年全国第一季度增速排名，部分省市有较大下滑，如D代表的湖北排名下滑最多．
②A、B、C分别代表的新疆、广西、青海位于西部地区，多为人口净流出或少量净流入，经济发展主要依靠本地劳动力供给，疫后复工复产效率相对较高，相对于2019年GDP增速排名位置靠前

25．已知线段AB=6cm，点M是线段AB上一动点，以AB为直径作⊙O，点C是圆周上一点且AC=4cm，连接CM，过点A作直线CM的垂线，交⊙O于点N，连接CN，设线段AM的长为xcm，线段AN的长为y1cm，线段CN的长为y2cm．
小华同学根据学习函数的经验，分别对函数y1，y2，随自变量x的变化而变化的规律进行了探究．
下面是该同学的探究过程，请补充完整：
(1)按照表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：
x/cm 0 1 2 3 4 5 6 
y1/cm 4.47 5.24 5.86 5.96        4.72 4.00 
y2/cm 6.00 5.86 5.23 3.98 2.46 1.06 0 

请你补全表格的相关数值，保留两位小数．
(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x，y1)，(x，y2)，并画出函数y1，y2的图象(函数y2的图象如图，请你画出y1的图象)

(3)结合画出的函数图象，解决问题：当△CAN是等腰三角形时，AM的长度约为       cm．

26．在平面直角坐标系中，已知抛物线y=ax2+2ax+c与x轴交于点A，B，且AB=4．抛物线与y轴交于点C，将点C向上移动1个单位得到点D．
(1)求抛物线对称轴；
(2)求点D纵坐标(用含有a的代数式表示)；
(3)已知点P(-4，4)，若抛物线与线段PD只有一个公共点，求a的取值范围．
27．点C为线段AB上一点，以AC为斜边作等腰Rt△ADC，连接BD，在△ABD外侧，以BD为斜边作等腰Rt△BED，连接EC．
(1)如图1，当∠DBA=30°时：
①求证：AC=BD；
②判断线段EC与EB的数量关系，并证明；
(2)如图2，当0°＜∠DBA＜45°时，EC与EB的数量关系是否保持不变？
对于以上问题，小牧同学通过观察、实验，形成了解决该问题的几种思路：
想法1：尝试将点D为旋转中心，过点D作线段BD垂线，交BE延长线于点G，连接CG；通过证明△ADB≌△CDG解决以上问题；
想法2：尝试将点D为旋转中心，过点D作线段AB垂线，垂足为点G，连接EG．通过证明△ADB∽△GDE解决以上问题；
想法3：尝试利用四点共圆，过点D作AB垂线段DF，连接EF，通过证明D、F、B、E四点共圆，利用圆的相关知识解决以上问题．
请你参考上面的想法，证明EC=EB(一种方法即可)．

28．过三角形的任意两个顶点画一条弧，若弧上的所有点都在该三角形的内部或边上，则称该弧为三角形的“形内弧”．

(1)如图，在等腰Rt△ABC中，∠A=90°，AB=AC=2．
①在图中画出一条Rt△ABC的形内弧；
②在Rt△ABC中，其形内弧的长度最长为      ．
(2)在平面直角坐标系中，点D(-2，0)，E(2，0)，F(0，1)．点M为△DEF形内弧所在圆的圆心．求点M纵坐标yM的取值范围；
(3)在平面直角坐标系中，点M(2，2
√3
)，点G为x轴上一点，点P为△OMG最长形内弧所在圆的圆心，求点P纵坐标yP的取值范围．
查看全部题目
【2020年北京市房山区中考数学二模试卷】标签
中考模拟试卷 最新试卷 北京试卷 房山区试卷 2020年试卷 初中试卷 九年级试卷 数学试卷
1 2 3 4 5 6 7 8 9
下载高清试卷