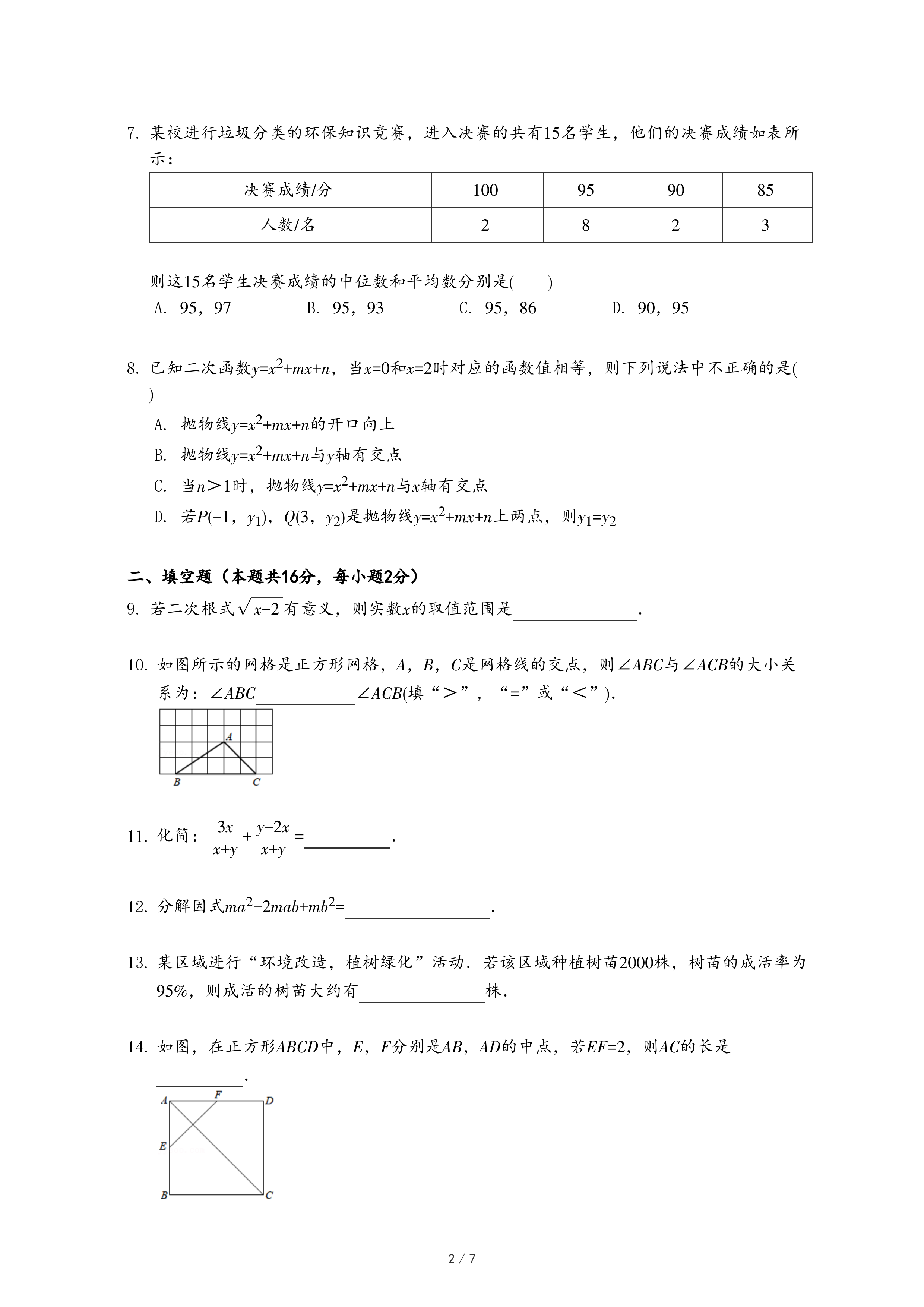
24.随着绿色出行意识增强,更多市民选择公共交通出行从市交通委获悉,目前,轨道交通多条线路缩短发车间隔,保障市民出行安全、便捷.
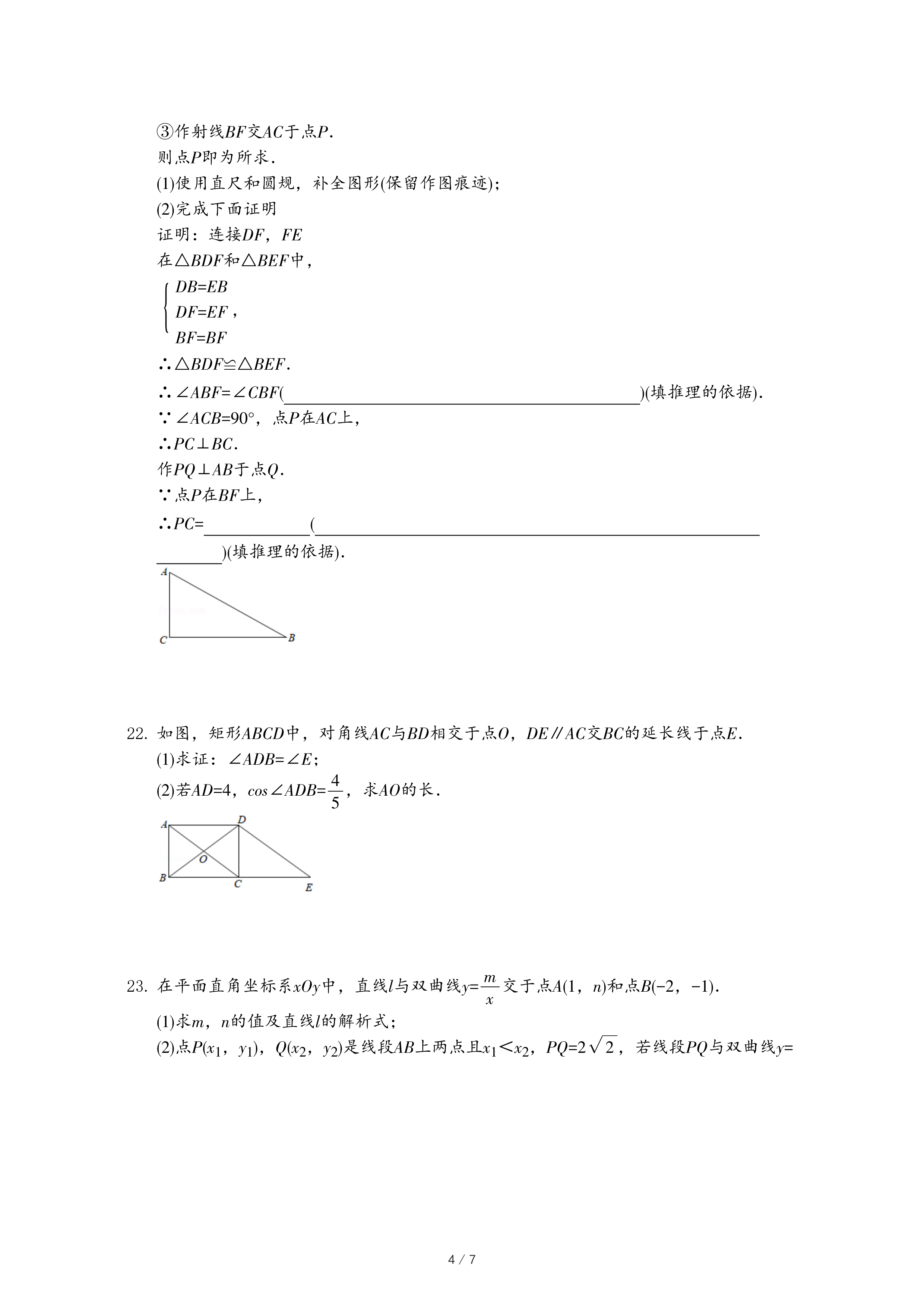
如图是地铁10号线由西钓鱼台站开往公主坟方向,工作日和双休日的列车时刻表(列车时刻表仅供参考,实际以现场列车运行情况为准).小明从西钓鱼台站乘10号线地铁(开往公主坟方向)出行,结合图中信息回答以下问题:
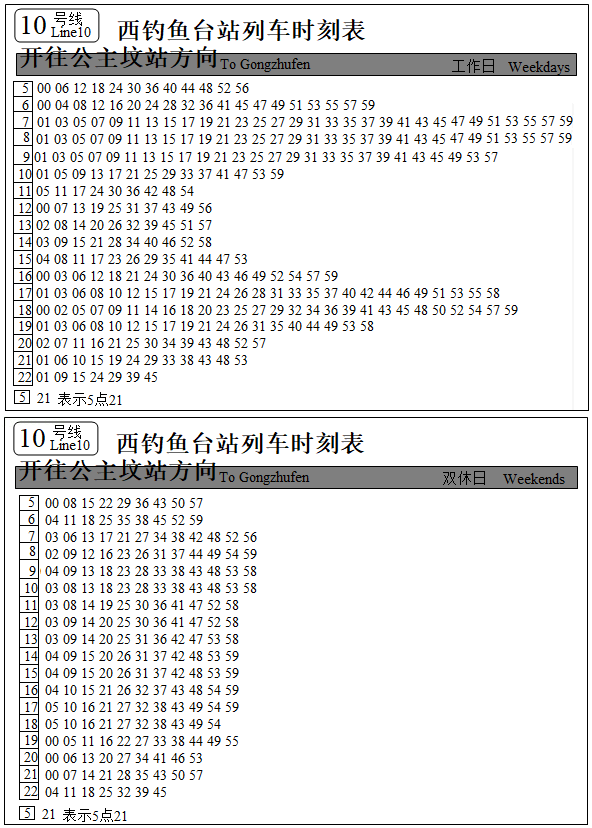
(1)工作日早晨7点01分-7点59分这段时间内,列车发车间隔为
分钟;
(2)下列说法中:
①双休日早晨6点04-6点59期间列车发车最小间隔为7分钟;
②设两个相邻整点之间为一个时间段,则工作日发车次数最少的时间段是22点-23点;
③设两个相邻整点之间为一个时间段,则双休日时,每个时间段的发车次数的众数为11;
④工作日10点01分-10点59分发车次数为12.
所有正确说法的序号是
;
(3)小明周一上午乘车时间为7点-7点10分之间,周二上午乘车时间为7点-7点06分之间.若这两天发车到站的时间与图中时间表一致,用画树状图或列表的方法,求小明这两天乘坐相同车次列车的概率(每天在同一时刻发车的列车视为相同车次)?