17．计算：(2-π)⁰+3^-1+||-2sin45°．

18．解不等式组：．

19．已知：直线l和l外一点P．求作：直线l的垂线，使它经过点P．
作法：①在直线l上任取两点A、B；
②分别以点A、B为圆心，AP，BP长为半径作弧，在直线l下方两弧交于点C；③作直线PC．所以直线PC为所求作的垂线．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连结AP、AC、BP、BC．
∵AP=AC，BP=BC，AB=AB，
∴△APB≌△ACB      (填推理依据)．
∴∠PAB=∠CAB，
∴PC⊥AB      (填推理依据)．

20．如图，C为∠AOB平分线上一点，CD∥OB交OA于点D．
求证：OD=CD．

21．已知a=3，求代数式(1-)÷的值．

22．如图，平行四边形ABCD的对角线AC，BD交于点O，AE⊥BC于点E，点F在BC延长线上，且CF=BE．
(1)求证：四边形AEFD是矩形；
(2)连接AF，若tan∠ABC=2，BE=1，AD=3，求AF的长．

23．在平面直角坐标系xOy中，反比例函数y=与一次函数y=kx+b相交于A(3，2)、B(-2，n)两点．
(1)求反比例函数和一次函数的表达式；
(2)过P(p，0)(p≠0)作垂直于x轴的直线，与反比例函数y=交于点C，与一次函数y=kx+b交于点D，若S_△COP=3S_△DOP，直接写出p的值．

24．垃圾分类是指按一定规定或标准将垃圾分类储存、投放和搬运，从而转变成公共资源的一系列活动的总称．做好垃圾分类有减少环境污染，节省土地资源等好处．现对某区30个小区某一天的厨余垃圾分出量和其他垃圾分出量的有关数据进行收集、整理、描述和分析．给出了部分信息：

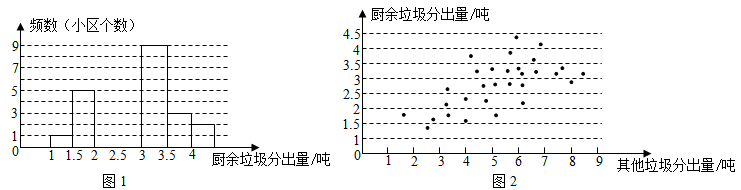
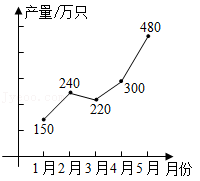
a.30个小区的厨余垃圾分出量的频数分布直方图，如图1(数据分成7组：1≤x＜1.5，1.5≤x＜2，2≤x＜2.5，2.5≤x＜3，3≤x＜3.5，3.5≤x＜4，4≤x≤4.5，单位：吨)；
b．各组厨余垃圾分出量平均数如表：(单位：吨)

c．厨余垃圾分出量在2.5≤x＜3这一组的数据是：(单位：吨)2.59；2.62；2.81；2.88；2.93；2.97．
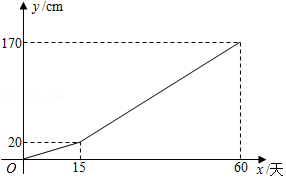
d.30个小区厨余垃圾分出量和其他垃圾分出量情况统计图，如图2．
e.30个小区中阳光小区的厨余垃圾分出量为2.97吨．
根据以上信息，回答下列问题：
(1)补全厨余垃圾分出量的频数分布直方图；
(2)阳光小区的厨余垃圾分出量在30个小区中由高到低排名第      ；阳光小区的其他垃圾分出量大约是      吨(结果保留一位小数)；
(3)30个小区厨余垃圾分出量平均数约为      吨(结果保留一位小数)．

25．如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．
(1)求证：∠FEB=∠ECF；
(2)若AB=6，sin∠CEB=，求CB和EF的长．

26．在平面直角坐标系xOy中，抛物线y=ax²-4ax+2(a＞0)与y轴交于点A．
(1)求点A的坐标及抛物线的对称轴；
(2)当0≤x≤5时，y的最小值是-2，求当0≤x≤5时，y的最大值；
(3)抛物线上的两点P(x₁，y₁)，Q(x₂，y₂)，若对于t＜x₁＜t+1，t+2＜x₂＜t+3，都有y₁≠y₂，直接写出t的取值范围．

27．已知：如图，在Rt△ABC中，∠ACB=90°，∠CAB=30°，P是AB边上任意一点，D是AB边的中点，连接CP，CD，并将PC绕点P逆时针旋转60°得到PE，连接AE．
(1)求证：CD=BC；
(2)①依题意补全图形；
②用等式表示线段PE与AE的数量关系，并证明．

28．对于平面直角坐标系xOy中的点P和图形G，给出如下定义：若在图形G上存在两个点M，N，且MN=2，使得以P，M，N为顶点的三角形为等边三角形，则称P为图形G的“正点”．已知A(2，0)，B(0，2)．
(1)在点C₁(-1，)，C₂(0，0)，C₃(2，)中，线段AB的“正点”是      ；
(2)直线y=k(x-1)+(k≠0)上存在线段AB的“正点”，求k的取值范围；
(3)以T(t，0)(t＜0)为圆心，2为半径作⊙T，若线段AB上总是存在⊙T的“正点”，直接写出t的取值范围．