17．计算：2tan60°-+()^-2+|1-|．

18．解不等式组，并写出它的所有整数解．

19．已知：如图，∠AOB和射线PN．
求作：射线PM，使得∠MPN=2∠AOB．
作法：①在射线OB上任取一点C，以点C为圆心，OC的长为半径画弧，交OA于点D；
②以点P为圆心，OC的长为半径画圆，交射线PN的反向延长线于点E；
③以点E为圆心，OD的长为半径画弧，在射线PN上方，交⊙P于点M；
④作射线PM．
所以射线PM就是所求作的射线．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连接CD，EM．
PM=PE=CD=CO，EM=OD．
∴△MEP≌△DOC(       )(填推理依据)．
∴∠MEP=∠DOC．
又∵∠MPN=2∠MEP(       )(填推理依据)．
∴∠MPN=2∠AOB．

20．已知关于x的一元二次方程mx²-(2m-1)x+m-2=0有两个不相等的实数根．
(1)求m的取值范围；
(2)若方程有一个根是0，求方程的另一个根．

21．如图，在四边形ABCD中，AD∥BC，AC⊥BD，垂足为O，过点D作BD的垂线交BC的延长线于点E．
(1)求证：四边形ACED是平行四边形；
(2)若AC=4，AD=2，cos∠ACB=，求BC的长．

22．在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象平行于直线y=x，且经过点A(2，2)．
(1)求这个一次函数的表达式；
(2)当x＜2时，对于x的每一个值，一次函数y=kx+b(k≠0)的值大于一次函数y=mx-1(m≠0)的值，直接写出m的取值范围．

23．如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点D为⌒AC的中点，对角线AC，BD交于点E，⊙O的切线AF交BD的延长线于点F，切点为A．
(1)求证：AE=AF；
(2)若AF=6，BF=10，求BE的长．

24．某公园内的人工湖里有一组小型喷泉，水柱从位于湖面上方的水枪喷出，水柱落于湖面的路径形状是抛物线．现测量出如下数据，在距离水枪水平距离为d米的地点，水柱距离湖面高度为h米．

请解决以下问题：
(1)在下面网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；
(2)请结合所画图象，水柱最高点距离湖面的高度是       米；
(3)求抛物线的表达式，并写出自变量的取值范围；
(4)现有一游船宽度为2米，顶棚到湖面的高度为2.5米．要求游船从喷泉水柱中间通过时，顶棚不碰到水柱．请问游船是否能符合上述要求通过？并说明理由．

25．为了进一步加强中小学国防教育，教育部研究制定了《国防教育进中小学课程教材指南》．某中学开展了形式多样的国防教育培训活动．为了解培训效果，该校组织七、八年级全体学生参加了国防知识竞赛(百分制)，并规定90分及以上为优秀，80～89分为良好，60～79分为及格.59分及以下为不及格．学校随机抽取了七、八年级各20名学生的成绩进行了整理与分析，下面给出了部分信息．
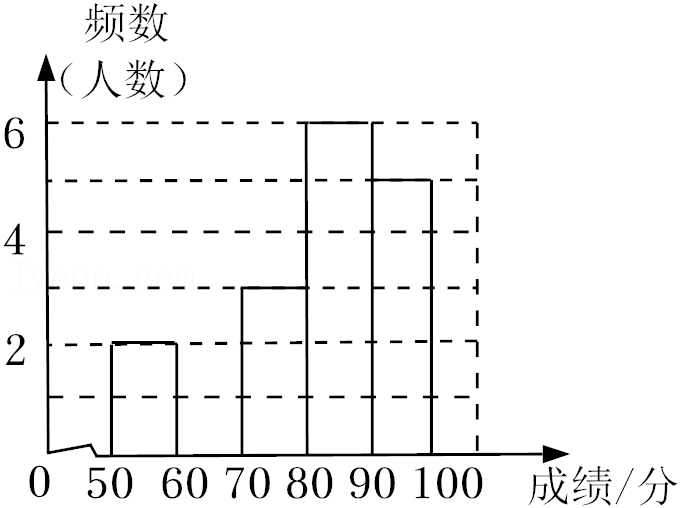
a．抽取七年级20名学生的成绩如下：
65 87 57 96 79 67 89 97 77 100 83 69 89 94 58 97 69 78 81 88
b．抽取七年级20名学生成绩的频数分布直方图如图(数据分成5组：50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100)；
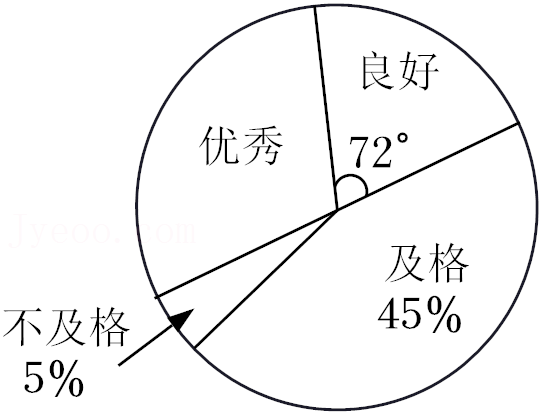
c．抽取八年级20名学生成绩的扇形统计图如图：
d．七年级、八年级各抽取的20名学生成绩的平均数、中位数、方差如表：

请根据以上信息，回答下列问题：
(1)补全七年级20名学生成绩的频数分布直方图，写出表中m的值；
(2)该校目前七年级有学生300人，八年级有学生200人，估计两个年级此次测试成绩达到优秀的学生各有多少人？
(3)你认为哪个年级的学生成绩较好，并说明理由．

26．在平面直角坐标系xOy中，点(2，-2)在抛物线y=ax²+bx-2(a＜0)上．
(1)求该抛物线的对称轴；
(2)已知点(n-2，y₁)，(n-1，y₂)，(n+1，y₃)在抛物线y=ax²+bx-2(a＜0)上．若0＜n＜1，比较y₁，y₂，y₃的大小，并说明理由．

27．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，EF垂直平分CD，分别交AC，BC于点E，F，连接DE，DF．
(1)求∠EDF的度数；
(2)用等式表示线段AE，BF，EF之间的数量关系，并证明．

28．在平面直角坐标系xOy中，⊙O的半径为2．对于直线l：y=x+1和线段BC，给出如下定义：若将线段BC沿直线l翻折可以得到⊙O的弦B'C'(B′，C'分别是B，C的对应点)，则称线段BC是以直线l为轴的⊙O的“关联线段”．例如：在图1中，线段BC是以直线l为轴的⊙O的“关联线段”．
(1)如图2，点B₁，C₁，B₂，C₂，B₃，C₃的横、纵坐标都是整数．在线段B₁C₁，B₂C₂，B₃C₃中，以直线l为轴的⊙O的“关联线段”是       ；
(2)△ABC是边长为a的等边三角形，点A(0，1)，若BC是以直线l为轴的⊙O的“关联线段”，求a的值；
(3)如果经过点P(-1，5)的直线上存在以直线l为轴的⊙O的“关联线段”，直接写出这条直线与y轴交点的纵坐标m的取值范围．