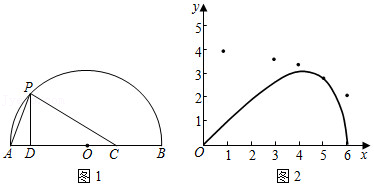
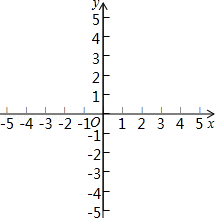25.如图,
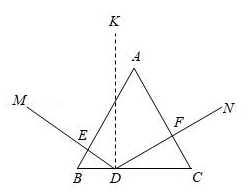
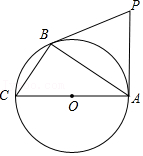
AB是以O为圆心,AB长为直径的半圆弧,点C是AB上一定点.点P是
AB上一动点,连接PA,PC,过点P作PD⊥AB于D.已知AB=6
cm,设A、P两点间的距离为x
cm,P、C两点间的距离为y
1cm,P、D两点间的距离为y
2cm.
小刚根据学习函数的经验,分别对函数y
1和y
2随自变量x变化而变化的规律进行了探究.下面是小刚的探究过程,请将它补充完整:
(1)按照表中自变量x的值进行取点、画图、测量,分别得到y
1和y
2与x的几组对应值:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y1/cm | 4.00 | 3.96 | m | 3.61 | 3.27 | 2.77 | 2.00 |
| y2/cm | 0.00 | 0.99 | 1.89 | 2.60 | 2.98 | 2.77 | 0.00 |
经测量,m的值是
;(保留一位小数)
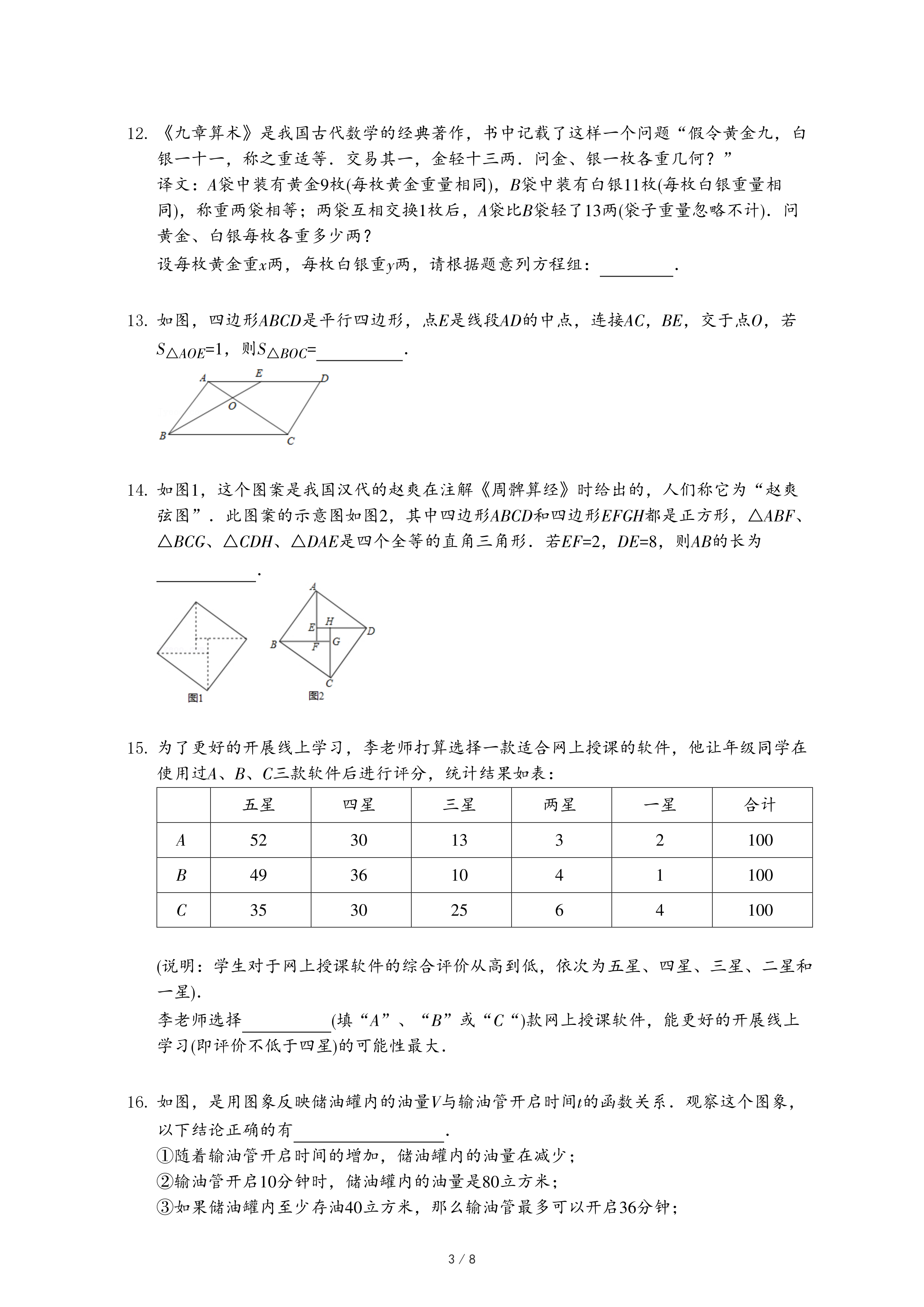
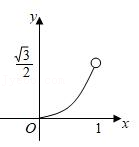
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y
1),点(x,y
2),并画出函数y
1,y
2的图象;
(3)结合函数图象,回答问题:△APC为等腰三角形时,AP的长度约为
cm.