首页 > 初中试卷 > 九年级试卷 > 九年级数学试卷 > 2020年九年级数学试卷 > 2020年北京九年级数学试卷 > 2020年北京数学中考模拟试卷

【2020年北京市密云区中考数学二模试卷】-第8页

试卷格式：2020年北京市密云区中考数学二模试卷.PDF
试卷热词：最新试卷、2020年、北京试卷、数学试卷、九年级试卷、中考模拟试卷、初中试卷
如何查看答案以及解析
下载试卷后，用微信扫一扫扫描试卷右上角二维码即可查看【2020年北京市密云区中考数学二模试卷】解析和视频讲解。
试卷题目
1．港珠澳大桥作为世界首例集桥梁、隧道和人工岛于一体的超级工程，创下了多项“世界之最”．它是世界上总体跨度最长的跨海大桥，全长55000米．其中海底隧道部分全长6700米，是世界最长的公路沉管隧道和唯一的深埋沉管隧道，也是我国第一条外海沉管隧道．其中，数字6700用科学记数法表示为(　　)

  • A. 67×102
  • B. 6.7×103
  • C. 6.7×104
  • D. 0.67×104
2．第二十四届冬季奥林匹克运动会将于2022年在北京举行，北京将成为历史上第一座既举办过夏奥会，又举办过冬奥会的城市．下面的图形是各届冬奥会会徽中的部分图案，其中是轴对称图形，但不是中心对称图形的是(　　)
  • A.
  • B.
  • C.
  • D.
3．如图，小林利用圆规在线段CE上截取线段CD，使CD=AB．若点D恰好为CE的中点，则下列结论中错误的是(　　)

  • A. CD=DE
  • B. AB=DE
  • C. CE=
    1
    2
    CD
  • D. CE=2AB
4．如图所示的四边形均为矩形或正方形，下列等式能够正确表示该图形面积关系的是(　　)

  • A. (a+b)2=a2+2ab+b2
  • B. (a+b)2=a2+2ab-b2
  • C. (a-b)2=a2-2ab+b2
  • D. (a-b)2=a2-2ab-b2
5．如图，在数轴上，点B在点A的右侧．已知点A对应的数为-1，点B对应的数为m．若在AB之间有一点C，点C到原点的距离为2，且AC-BC=2，则m的值为(　　)

  • A. 4
  • B. 3
  • C. 2
  • D. 1
6．如果x2+2x-2=0，那么代数式
1
x-2
•
x2-4x+4
x
-
x
x+2
的值为(　　)
  • A. -2
  • B. -1
  • C. 1
  • D. 2
7．新冠疫情发生以来，为保证防控期间的口罩供应，某公司加紧转产，开设多条生产线争分夺秒赶制口罩，从最初转产时的陌生，到正式投产后达成日均生产100万个口罩的产能．不仅效率高，而且口罩送检合格率也不断提升，真正体现了“大国速度”．以下是质监局对一批口罩进行质量抽检的相关数据，统计如下：
抽检数量n/个 20 50 100 200 500 1000 2000 5000 10000 
合格数量m/个 19 46 93 185 459 922 1840 4595 9213 
口罩合格率
m
n
 		0.950 0.920 0.930 0.925 0.918 0.922 0.920 0.919 0.921 

下面四个推断合理的是(　　)
  • A. 当抽检口罩的数量是10000个时，口罩合格的数量是9213个，所以这批口罩中“口罩合格”的概率是0.921
  • B. 由于抽检口罩的数量分别是50和2000个时，口罩合格率均是0.920，所以可以估计这批口罩中“口罩合格”的概率是0.920
  • C. 随着抽检数量的增加，“口罩合格”的频率总在0.920附近摆动，显示出一定的稳定性，所以可以估计这批口罩中“口罩合格”的概率是0.920
  • D. 当抽检口罩的数量达到20000个时，“口罩合格”的概率一定是0.921
8．如图，点C、A、M、N在同一条直线l上．其中，△ABC是等腰直角三角形，∠B=90°，四边形MNPQ为正方形，且AC=4，MN=2，将等腰Rt△ABC沿直线l向右平移．若起始位置为点A与点M重合，终止位置为点C与点N重合．设点A平移的距离为x，两个图形重叠部分的面积为y，则y与x的函数图象大致为(　　)

  • A.
  • B.
  • C.
  • D.
9．分解因式：3ax2-12a=      ．
10．若二次根式
√x-4
在实数范围内有意义，则x的取值范围是      ．
11．如图，已知菱形ABCD，通过测量、计算得菱形ABCD的面积约为      cm2．(结果保留一位小数)

12．如图∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠EAB=120°，则∠1+∠2+∠3+∠4=      ．

13．已知“若a＞b，则ac＜bc”是真命题，请写出一个满足条件的c的值是      ．
14．如图，小军在A时测量某树的影长时，日照的光线与地面的夹角恰好是60°，当他在B时测量该树的影长时，日照的光线与地面的夹角是30°，若两次测得的影长之差DE为4m，则树的高度为      m．（结果精确到0.1，参考数据：
√2
≈1.414，
√3
≈1.732）

15．已知：点A、点B在直线MN的两侧．(点A到直线MN的距离小于点B到直线MN的距离)．
如图，
(1)作点B关于直线MN的对称点C；
(2)以点C为圆心，
1
2
BC的长为半径作⊙C，交BC于点E；
(3)过点A作⊙C的切线，交⊙C于点F，交直线MN于点P；
(4)连接PB、PC．
根据以上作图过程及所作图形，下列四个结论中：
①PE是⊙C的切线； ②PC平分⌒EF；③PB=PC=PF； ④∠APN=2∠BPN．
所有正确结论的序号是      ．

16．某校举办初中生数学素养大赛，比赛共设四个项目：七巧拼图、趣题巧解、数学应用和魔方复原，每个项目得分都按一定百分比折算后记入总分，并规定总分在85分以上(含85分)设为一等奖．如表为甲、乙、丙三位同学的得分情况(单位：分)，其中甲的部分信息不小心被涂黑了．
项目得分项目学生 七巧拼图 趣题巧解 数学应用 魔方复原 折算后总分 
甲 66 95  68  
乙 66 80 60 68 70 
丙 66 90 80 68 80 

据悉，甲、乙、丙三位同学的七巧拼图和魔方复原两项得分折算后的分数之和均为20分．设趣题巧解和数学应用两个项目的折算百分比分别为x和y，请用含x和y的二元一次方程表示乙同学“趣题巧解和数学应用”两项得分折算后的分数之和为      ；如果甲获得了大赛一等奖，那么甲的“数学应用”项目至少获得      分．
17．计算：
3√8
-(
1
3
)-1+|5-
√3
|-6tan30°．
18．解不等式组：
19．如图，在▱ABCD中，DB=CD，∠C=70°，AE⊥BD于点E．试求∠DAE的度数．

20．已知关于x的一元二次方程x2+2x+m-4=0有两个实数根．
(1)求m的取值范围；
(2)写出一个满足条件的m的值，并求出此时方程的根．
21．如图，在△AOC中，OA=OC，OD是AC边上的中线．延长AO至点B，作∠COB的角平分线OH，过点C作CF⊥OH于点F．
(1)求证：四边形CDOF是矩形；
(2)连接DF，若cosA=
3
5
，CF=8，求DF的长．

22．在平面直角坐标系xOy中，直线l：y=x+b与反比例函数y=
4
x
在第一象限内的图象交于点A(4，m)．
(1)求m、b的值；
(2)点B在反比例函数的图象上，且点B的横坐标为1．若在直线l上存在一点P(点P不与点A重合)，使得AP≤AB，结合图象直接写出点P的横坐标xP的取值范围．

23．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D在⊙O上，AC平分∠BAD，过点C的切线交直径AB的延长线于点E，连接AD、BC．
(1)求证：∠BCE=∠CAD；
(2)若AB=10，AD=6，求CE的长．

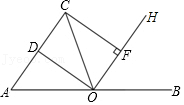
24．“垃圾分类就是新时尚”．树立正确的垃圾分类观念，促进青少年养成良好的文明习惯，对于增强公共意识，提升文明素质具有重要意义．为了调查学生对垃圾分类知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩(百分制，单位：分)，并对数据(成绩)进行了整理、描述和分析，下面给出了部分信息．
a．甲、乙两校学生样本成绩频数分布表及扇形统计图如图：
甲校学生样本成绩频数分布表(表1)
成绩m(分) 频数 频率 
50≤m＜60 a 0.10 
60≤m＜70 b c 
70≤m＜80 4 0.20 
80≤m＜90 7 0.35 
90≤m≤100 2 d 
合计 20 1.0 

b．甲、乙两校学生样本成绩的平均分、中位数、众数、方差如表所示：(表2)
学校 平均分 中位数 众数 方差 
甲 76.7 77 89 150.2 
乙 78.1 80 n 129.49 

其中，乙校20名学生样本成绩的数据如下：
54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91
请根据所给信息，解答下列问题：
(1)表1中c=      ；表2中的众数n=      ；
(2)乙校学生样本成绩扇形统计图中，70≤m＜80这一组成绩所在扇形的圆心角度数是      度；
(3)在此次测试中，某学生的成绩是79分，在他所属学校排在前10名，由表中数据可知该学生是      校的学生(填“甲”或“乙”)，理由是      ；
(4)若乙校1000名学生都参加此次测试，成绩80分及以上为优秀，请估计乙校成绩优秀的学生约为      人．

25．有这样一个问题：探究函数y=
1
2
x3-4x+1的图象与性质．
文文根据学习函数的经验，对函数y=
1
2
x3-4x+1的图象与性质进行了探究．
下面是文文的探究过程，请补充完整：
(1)函数y=
1
2
x3-4x+1的自变量x的取值范围是      ；
(2)如表是y与x的几组对应值：
x … -3 -2 -
3
2
 		-1 -
1
2
 		0 
1
2
 		1 
3
2
 		2 3 … 
y … -
1
2
 		5 
85
16
 
9
2
 
47
16
 		1 -
15
16
 		m -
53
16
 		-3 
5
2
 		… 

则m的值为      ；
(3)如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
(4)请你根据探究二次函数与一元二次方程关系的经验，结合图象直接写出方程
1
2
x3-4x=-1的正数根约为      ．(结果精确到0.1)

26．在平面直角坐标系xOy中，抛物线C1：y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C．点B的坐标为(3，0)，将直线y=kx沿y轴向上平移3个单位长度后，恰好经过B、C两点．
(1)求k的值和点C的坐标；
(2)求抛物线C1的表达式及顶点D的坐标；
(3)已知点E是点D关于原点的对称点，若抛物线C2：y=ax2-2(a≠0)与线段AE恰有一个公共点，结合函数的图象，求a的取值范围．

27．已知：MN是经过点A的一条直线，点C是直线MN左侧的一个动点，且满足60°＜∠CAN＜120°，连接AC，将线段AC绕点C顺时针旋转60°，得到线段CD，在直线MN上取一点B，使∠DBN=60°．

(1)若点C位置如图1所示．
①依据题意补全图1；
②求证：∠CDB=∠MAC；
(2)连接BC，写出一个BC的值，使得对于任意一点C，总有AB+BD=3，并证明．
28．在平面直角坐标系xOy中，点A的坐标为(x1，y1)，点B的坐标为(x2，y2)，且x1≠x2，y1=y2．给出如下定义：若平面上存在一点P，使△APB是以线段AB为斜边的直角三角形，则称点P为点A、点B的“直角点”．
(1)已知点A的坐标为(1，0)．
①若点B的坐标为(5，0)，在点P1(4，3)、P2(3，-2)和P3(2，
√3
)中，是点A、点B的“直角点”的是      ；
②点B在x轴的正半轴上，且AB=2
√2
，当直线y=-x+b上存在点A、点B的“直角点”时，求b的取值范围；
(2)⊙O的半径为r，点D(1，4)为点E(0，2)、点F(m，n)的“直角点”，若使得△DEF与⊙O有交点，直接写出半径r的取值范围．

查看全部题目
【2020年北京市密云区中考数学二模试卷】标签
中考模拟试卷 最新试卷 北京试卷 2020年试卷 初中试卷 九年级试卷 数学试卷
1 2 3 4 5 6 7 8 9
下载高清试卷