


| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
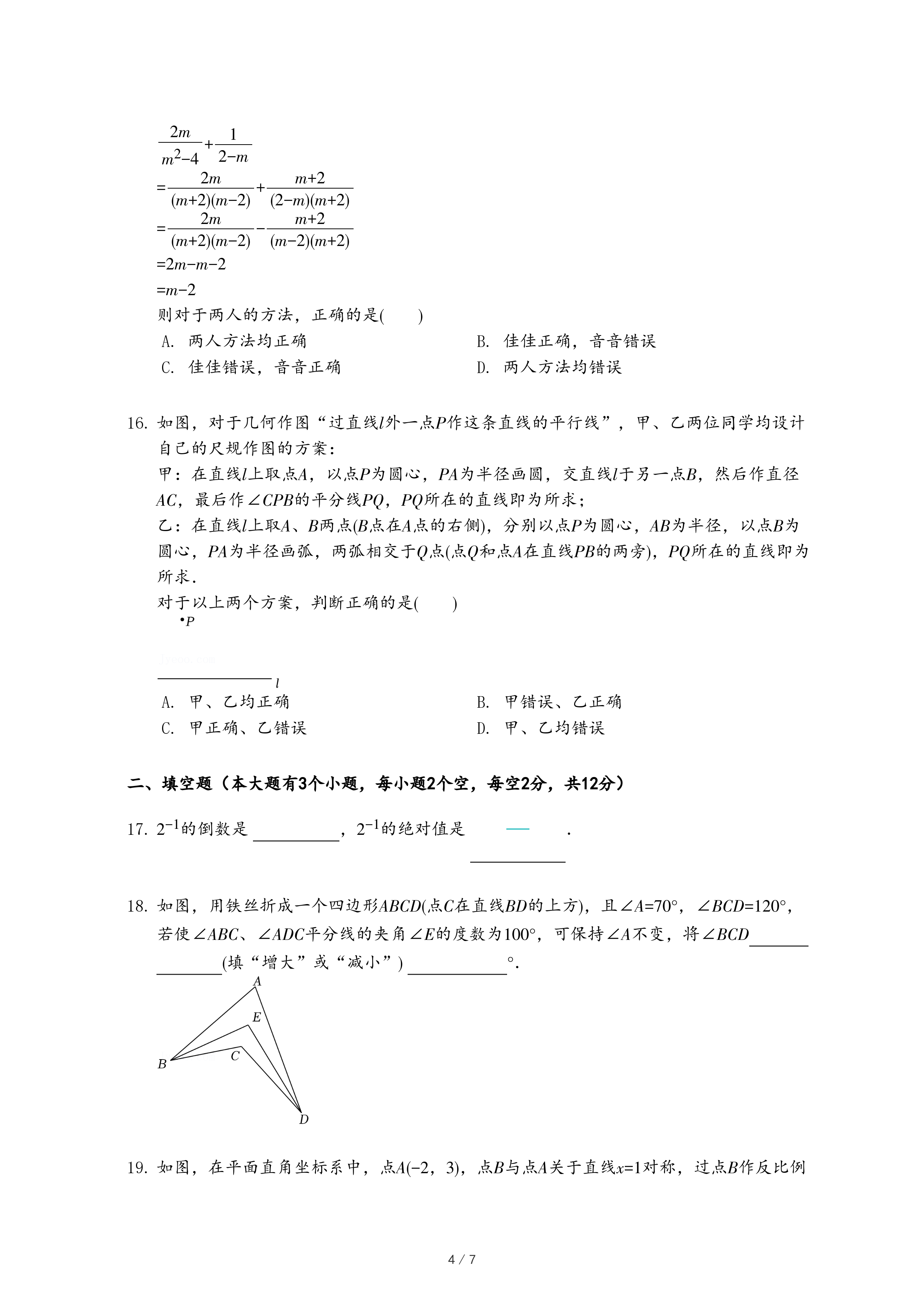
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |




| 2m |
| m2-4 |
| 1 |
| 2-m |
| 2m |
| m2-4 |
| 1 |
| 2-m |
| 2m |
| m2-4 |
| 1 |
| m+2 |
| 2m |
| (m+2)(m-2) |
| m-2 |
| (m+2)(m-2) |
| 2m-m+2 |
| (m+2)(m-2) |
| 1 |
| m-2 |
| 2m |
| m2-4 |
| 1 |
| 2-m |
| 2m |
| (m+2)(m-2) |
| m+2 |
| (2-m)(m+2) |
| 2m |
| (m+2)(m-2) |
| m+2 |
| (m-2)(m+2) |

| m |
| x |
| m |
| x |
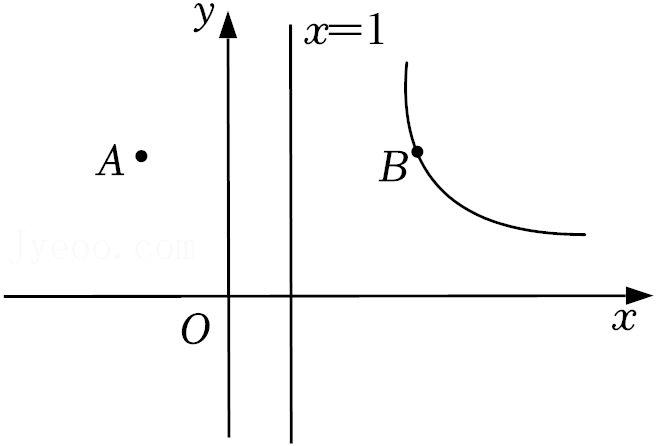
| 5 |
| 2 |
| x(件) | 10 | 50 |
| P(元) | 70 | 38 |