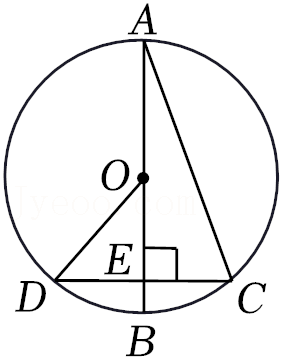
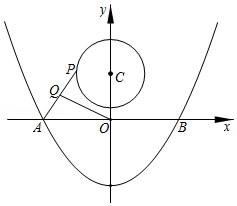
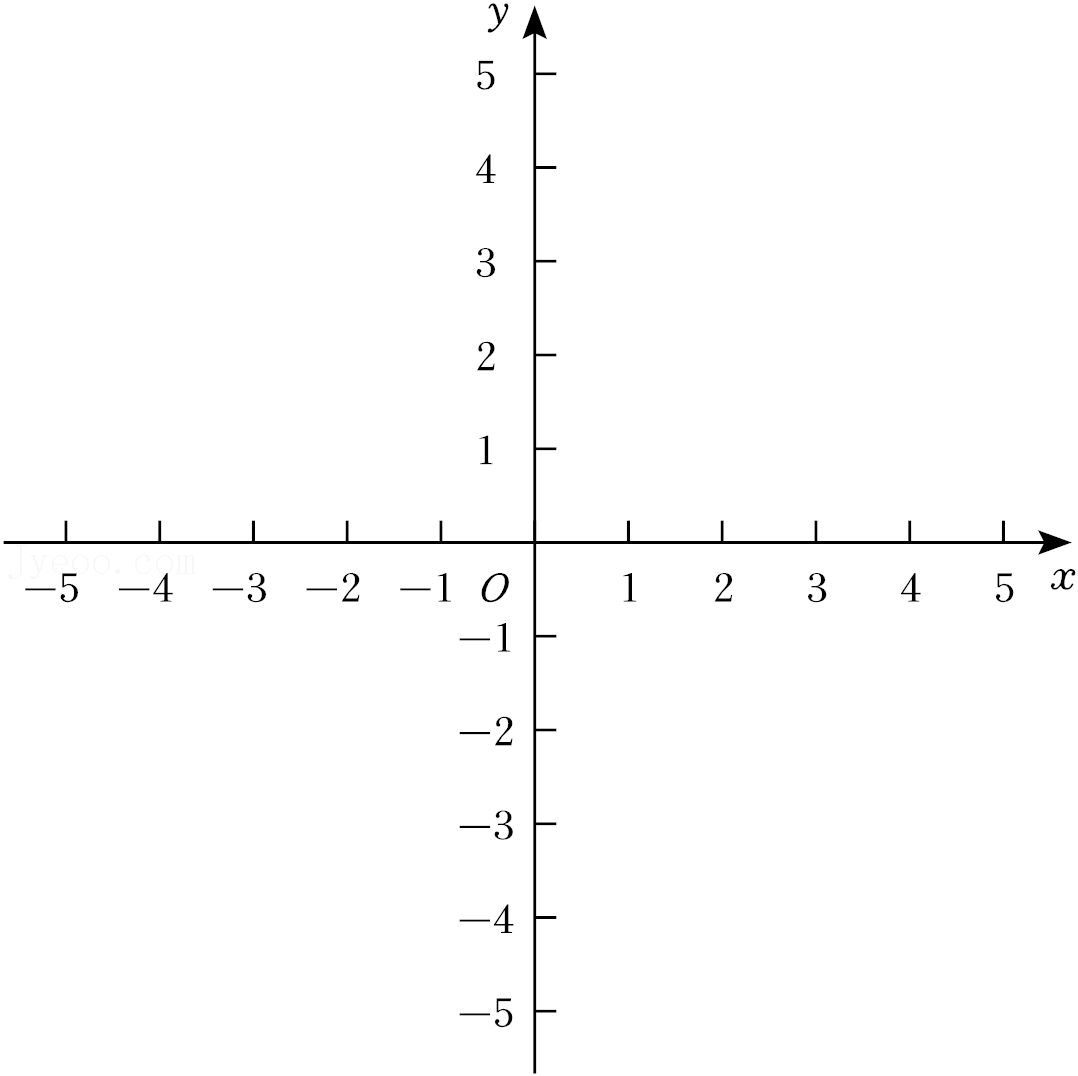
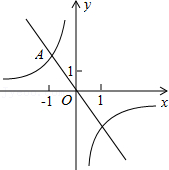28.如图,在平面直角坐标系xOy中,C(0,2),⊙C的半径为1.如果将线段AB绕原点O逆时针旋转α(0°<α<180°)后的对应线段A'B'所在的直线与⊙C相切,且切点在线段A′B′上,那么线段AB就是⊙C的“关联线段”,其中满足题意的最小α就是线段AB与⊙C的“关联角”.
(1)如图1,如果A(2,0),线段OA是⊙C的“关联线段”,那么它的“关联角”为
°.
(2)如图2,如果A
1(-3,3)、B
1(-2,3),A
2(1,1)、B
2(3,2),A
3(3,0)、B
3(3,-2).
那么⊙C的“关联线段”有
(填序号,可多选).
①线段A
1B
1②线段A
2B
2③线段A
3B
3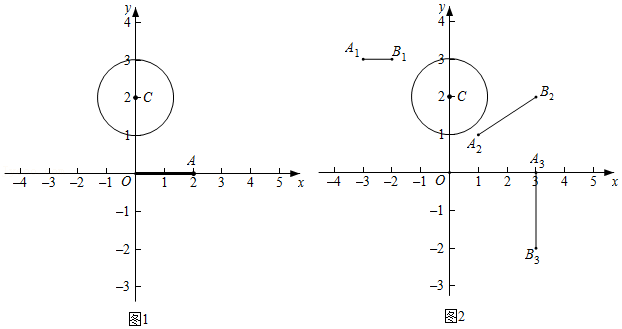
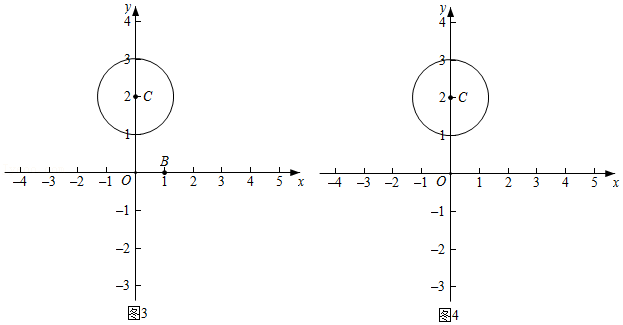
(3)如图3,如果B(1,0)、D(t,0),线段BD是⊙C的“关联线段”,那么t的取值范围是
.
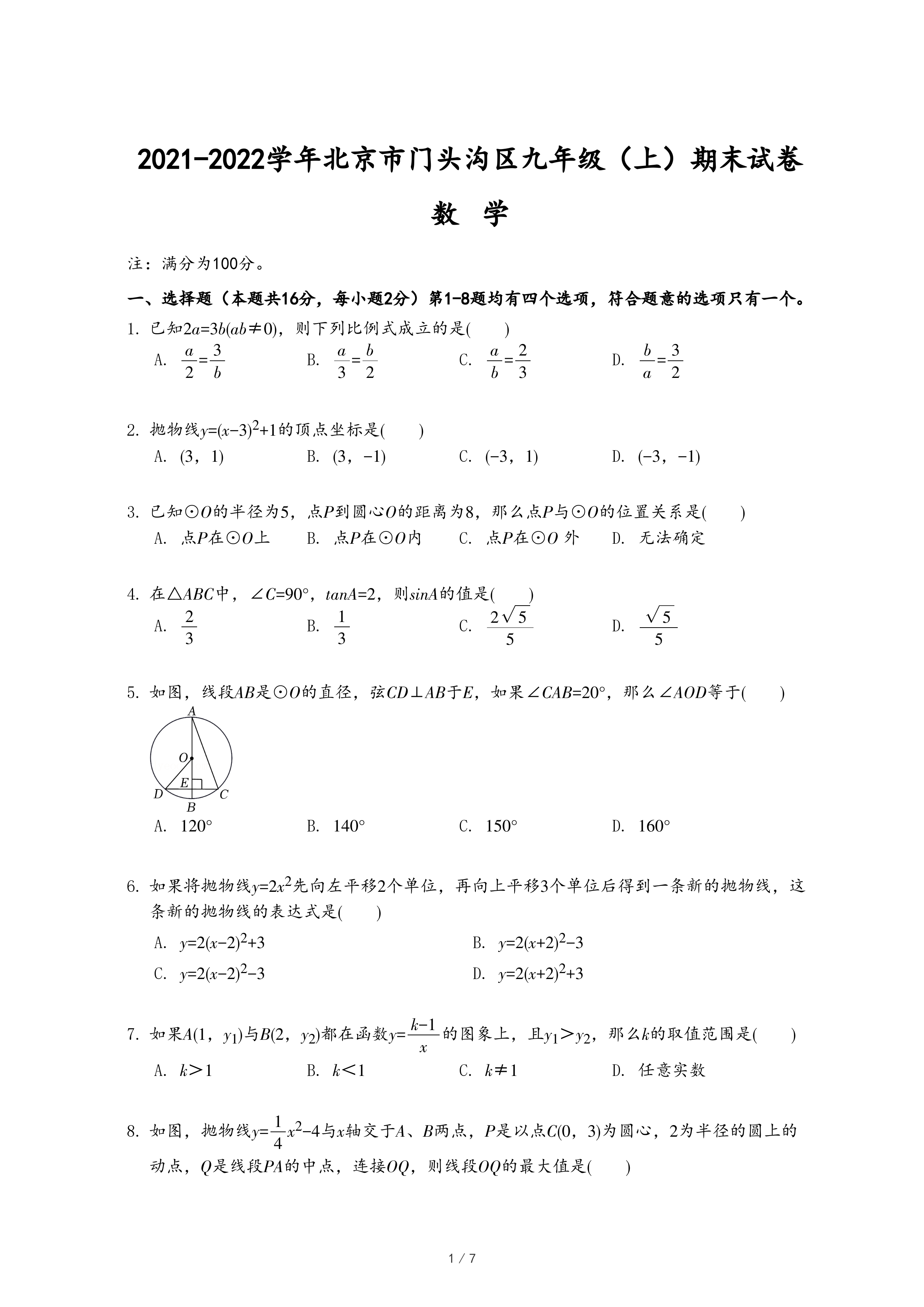
(4)如图4,如果点M的横坐标为m,且存在以M为端点,长度为
√3
的线段是⊙C的“关联线段”,那么m的取值范围是
.