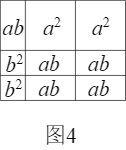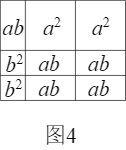23.阅读理解下列材料:
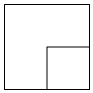
“数形结合“是一种非常重要的数学思想.在学习“整式的乘法”时,我们通过构造几何图形,用“等积法”直观地推导出了完全平方和公式:(a+b)
2=a
2+2ab+b
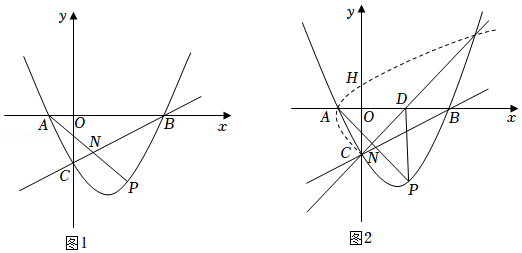
2(如图1).所谓“等积法”就是用不同的方法表示同一个图形的面积,从而得到一个等式.如图1,从整体看是一个边长为a+b的正方形,其面积为(a+b)
2.从局部看由四部分组成,即:一个边长为a的正方形,一个边长为b的正方形,两个长、宽分别为a,b的长方形.这四部分的面积和为a
2+2ab+b
2.因为它们表示的是同一个图形的面积,所:以这两个代数式应该相等,即(a+b)
2=a
2+2ab+b.
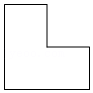
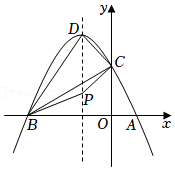
同理,图2可以得到一个等式:(a+b)(2a+b)=2a
2+3ab+b
2.
根据以上材料提供的方法,完成下列问题:
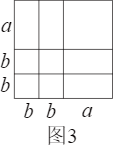
(1)由图3可得等式:
;
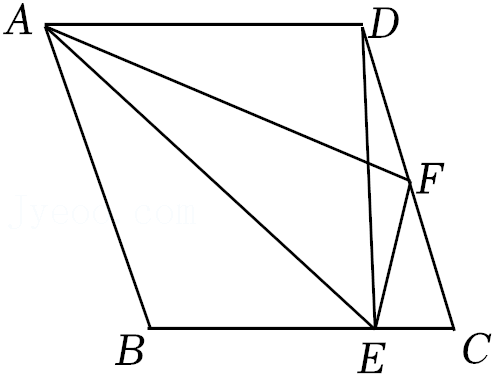
(2)由图4可得等式:
;
(3)若a>0,b>0,c>0,且a+b+c=9,ab+bc+ac=26,求a
2+b
2+c
2的值.
①为了解决这个问题,请你利用数形结合思想,仿照前面的方法在下方空白处画出相应的几何图形,通过这个几何图形得到一个含有a,b,c的等式.
②根据你画的图形可得等式:
.
③利用①的结论,求a
2+b
2+c
2的值.