17．计算：
(1)(a-b)²-2a(a+b)；
(2)÷(1-)．

18．如图，在▱ABCD中AD＞AB．
(1)尺规作图：在AD上截取AE，使得AE=AB．作∠ADC的平分线交BC于点F(保留作图痕迹，不写作法)；
(2)在(1)所作图形中，连接BE，求证：四边形BEDF是平行四边形．(请补全下面的证明过程，不写证明理由)．
证明：∵DF平分∠ADC，
∴      
∵在▱ABCD中，BC∥AD，
∴      
∴∠CDF=∠CFD，
∴CD=CF．
∵在▱ABCD中，AB=CD，
又∵AE=AB，
∴AE=CF．
∵在▱ABCD中，AD=BC，
∴AD-AE=BC-CF，
即       
又∵      
∴四边形BEDF是平行四边形．

19．一次函数y=-x+b与反比例函数y=(k≠0)相交于A(-1，4)、B两点．
(1)求一次函数和反比例函数的解析式，并在网格中画出一次函数和反比例函数的图象；
(2)点C(2，m)是反比例函数图象上一点，连接AC，BC，求△ABC的面积；
(3)根据图象，直接写出关于x的不等式-x+b≤的解集．

20．2022年4月2日，中国人民银行召开数字人民币研发试点工作座谈会，在现有试点地区基础上增加重庆市等6个城市作为试点地区，某校数学兴趣小组为了调查七、八年级同学们对数字人民币的了解程度，设计了一张含10个问题的调查问卷，在该校七、八年级中各随机抽取20名学生进行调查，并将结果整理、描述和分析，下面给出了部分信息．
七年级20名学生答对的问题数量为：

八年级20名学生答对的问题数量的条形统计图如图：

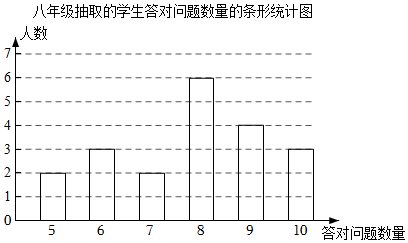
七、八年级抽取的学生答对问题数量的平均数、众数、中位数、答对8题及以上人数所占百分比如表所示：两组数据的平均数，众数，中位数，优秀率如表所示：

根据以上信息，解答下列问题：
(1)直接写出上述表中的a，b，c的值；
(2)根据上述数据，你认为该校七、八年级中哪个年级的学生更了解数字人民币？请说明理由(写出一条理由即可)；
(3)若答对7题及以上视为比较了解数字人民币，该校七年级有800名学生，八年级有700名学生，估计该校七年级和八年级比较了解数字人民币的学生总人数是多少？

21．小张是“科技协会”的一名会员，他设计了一款距离测量仪器，这款仪器的最大测量距离为34米(测量距离为两点所连线段的长度)．为了测试这款仪器的性能，小张来到一座小山坡．从山脚A处开始，作为测量点，手持仪器沿斜坡AB向上走．已知AC⊥BC，AC=19.2米，BC=8米．
(1)求tanA的值；
(2)小张到达B后继续测试，先走一段水平路面BD，BD∥AC，长为2.8米，再沿另一斜坡DE向上走，直到G点，此时G，A两点之间达到最大测量距离34米，且斜坡DE的仰角为45°．请求出DG的长度．(结果保留一位小数，在整个测量过程中，小张所走的路线在同一平面内：≈1.41，≈1.73)

22．农历虎年之际，某社区为了突出浓浓年味，计划购买A与B两种贴花共500张．已知A贴花的售价是每张15元，B贴花的售价是每张30元，共花费9000元．
(1)求计划购买多少张B贴花？
(2)为了节省费用，社区工作人员最终在网上购买，A贴花每张售价减少了，B贴花每张售价也便宜了m元．现在在(1)的基础上购买B贴花的数量增加了m张，总数量不变，并且总费用比原计划减少了(2000+10m)元，求m的值．

23．一个四位数m=1000a+100b+10c+d(其中1≤a，b，c，d≤9，且均为整数)，若a+b=k(c-d)，且k为整数，称m为“k型数”．例如，4675：4+6=5×(7-5)，则4675为“5型数”；3526：3+5=-2×(2-6)，则3526为“-2型数”．
(1)判断1731与3213是否为“k型数”，若是，求出k；
(2)若四位数m是“3型数”，m-3是“-3型数”，将m的百位数字与十位数字交换位置，得到一个新的四位数m′，m′也是“3型数”，求满足条件的所有四位数m．

24．如图，在平面直角坐标系中，抛物线y=x²+x-3交x轴于点A，点B(点A在点B的左侧)，交y轴于点C，连接AC，BC．P是第三象限内抛物线上一动点，过P作PE∥y轴交AC于点E，过E作EF∥BC交x轴于点F．
(1)求△ABC的面积；
(2)求PE+EF+FO的最大值及此时点P的坐标；
(3)将抛物线y=x²+x-3平移，使得新抛物线的顶点为(2)中求得的点P，点Q为x轴下方的新抛物线上一点，R为x轴上一点，直接写出所有使得以点A，C，Q，R为顶点的四边形是平行四边形的点R的坐标．

25．如图，在△ABC中，点D，E分别在BC，AC上，连接AD，AD=DC，点E为AC中点，连接BE交AD于点N，BN=NE．
(1)如图1，若∠ANE=90°，AE=4，求DC的长；
(2)如图2，延长BA至点M，连接ME，AN=ME，若∠ABC=45°，求证：AM+NE=AN；
(3)如图3，延长BA至点M，连接ME，ME=3，∠ADC=∠MEB=90°，点N为AB中点，连接NE，将△BNE沿NE翻折得到△B′NE，点F，G分别为NE，EB′上的动点(不与端点重合)，连接AF，FG，连接MG交直线AE于点H，当AF+FG取得最小值时，直接写出的值．