










| 液体名称 | 液态氧 | 液态氢 | 液态氮 | 液态氦 |
| 沸点(℃) | -183 | -253 | -196 | -268.9 |
√x-2022 |
| x-2022 |
| 1 |
| 7 |
| 4 |
| x |

| 2400 |
| x |
| 2400 |
| x+40 |
| 2400 |
| x |
| 2400 |
| x+40 |
| 2400 |
| x+2 |
| 2400 |
| x |
| 2400 |
| x+2 |
| 2400 |
| x |
| l6 |
| 2R |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 2y |
| y2-1 |
| 1 |
| y-1 |
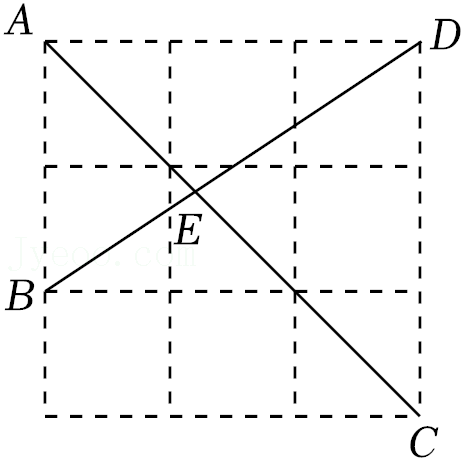
| EF |
| AB |
| 1 |
| 4 |
| AD |
| AB |
德国数学家高斯(Gauss)在上小学时就已经找到快速计算1+2+3+⋯+99+100=5050的方法,今天我们可以将高斯的做法归纳如下:设s=1+2+3+…+n.①;则s=n+(n-1)+(n-2)+…+1.②;①+②,得2s=(n+1)+(n+1)+(n+1)+⋯+(n+1)=n(n+1).所以s=
|
| 印数a(千册) | 0≤a<5 | a≥5 |
| 彩色(元/张) | 2.1 | 2 |
| 黑白(元/张) | 0.8 | 0.5 |