2022年北京市西城区中考数学二模试卷-乐乐课堂

1．如图是某几何体的展开图，该几何体是(　　)

A. 圆柱
B. 长方体
C. 圆锥
D. 三棱锥

2．2022年4月28日，京杭大运河实现全线通水．京杭大运河是中国古代劳动人民创造的一项伟大工程，它南起余杭(今杭州)，北到涿郡(今北京)，全长约1800000m．将1800000用科学记数法表示应为(　　)

A. 0.18×10⁷
B. 1800×10³
C. 18×10⁵
D. 1.8×10⁶

3．下列图形中，既是中心对称图形也是轴对称图形的是(　　)

A.
B.
C.
D.

4．在同一条数轴上分别用点表示实数-1.5，0，-

√11

，|-4|，则其中最左边的点表示的实数是(　　)

A. -
√11
B. 0
C. -1.5
D. |-4|

5．学校图书馆的阅读角有一块半径为3m，圆心角为120°的扇形地毯，这块地毯的面积为(　　)

A. 9πm²
B. 6πm²
C. 3πm²
D. πm²

6．如图，在平行四边形ABCD中，点E在BA的延长线上，AB=2AE，EC，BD交于点F．若BD=10，则DF的长为(　　)

A. 3.5
B. 4.5
C. 4
D. 5

7．一条观光船沿直线向码头前进，下表记录了4个时间点观光船与码头的距离，其中t表示时间，y表示观光船与码头的距离．

t/min	0	3	6	9
y/m	675	600	525	450

如果观光船保持这样的行进状态继续前进，那么从开始计时到观光船与码头的距离为150m时，所用时间为(　　)

A. 25min
B. 21min
C. 13min
D. 12min

8．教练将某射击运动员50次的射击成绩录入电脑，计算得到这50个数据的平均数是7.5，方差是1.64．后来教练核查时发现其中有2个数据录入有误，一个错录为6环，实际成绩应是8环；另一个错录为9环，实际成绩应是7环．教练将错录的2个数据进行了更正，更正后实际成绩的平均数是x，方差是s²，则(　　)

A. x＜7.5，s²=1.64
B. x=7.5，s²＞1.64
C. x＞7.5，s²＜1.64
D. x=7.5，s²＜1.64

9．若

1

x-4

在实数范围内有意义，则实数x的取值范围是．

10．方程组的解为．

11．如图，将直角三角形纸片ABC进行折叠，使直角顶点A落在斜边BC上的点E处，并使折痕经过点C，得到折痕CD．若∠CDE=70°，则∠B= °．

12．用一个a的值说明命题“若a＞0，则a²＞

1

a

”是错误的，这个值可以是a= ．

13．如图，在△ABC中，D，E分别为AB，AC的中点，点F在线段DE上，且AF⊥BF．若AB=4，BC=7，则EF的长为．

14．将抛物线y=2x²向下平移b(b＞0)个单位长度后，所得新抛物线经过点(1，-4)，则b的值为．

15．如图，⊙O是△ABC的外接圆，OB=

√13

，BC=4，则tanA的值为．

16．如图，在8个格子中依次放着分别写有字母a～h的小球．

甲、乙两人轮流从中取走小球，规则如下：
①每人首次取球时，只能取走2个或3个球；后续每次可取走1个，2个或3个球；
②取走2个或3个球时，必须从相邻的格子中取走；
③最后一个将球取完的人获胜．
(1)若甲首次取走写有b，c，d的3个球，接着乙首次也取走3个球，则 (填“甲”或“乙”)一定获胜；
(2)若甲首次取走写有a，b的2个球，乙想要一定获胜，则乙首次取球的方案是．

17．计算：|-

√2

|+2cos45°-

√8

+(

1

3

)^-2．

18．解不等式：

5x-2

6

＜

x

2

+1，并写出它的正整数解．

19．已知x²+x-5=0，求代数式(

1

x

+

1

x+1

)•

5

6x+3

的值．

20．已知：如图，△ABC．
求作：点D(点D与点B在直线AC的异侧)，使得DA=DC，且∠ADC+∠ABC=180°．
作法：①分别作线段AC的垂直平分线l₁和线段BC的垂直平分线l₂，直线l₁与l₂交于点O；
②以点O为圆心，OA的长为半径画圆，⊙O与l₁在直线BC上方的交点为D；
③连接DA，DC．
所以点D就是所求作的点．
(1)使用直尺和圆规，依作法补全图形(保留作图痕迹)；
(2)完成下面的证明．
证明：连接OA，OB，OC．
∵直线l₁垂直平分AC，点O，D都在直线l₁上，
∴OA=OC，DA=DC．
∵直线l₂垂直平分BC，点O在直线l₂上，
∴ = ．
∴OA=OB=OC．
∴点A，B，C都在⊙O上．
∵点D在⊙O上，
∴∠ADC+∠ABC=180°．( )(填推理的依据)

21．已知关于x的一元二次方程

1

2

x²-mx+m-5=0．
(1)求证：此方程总有两个不相等的实数根；
(2)若m为整数，且此方程的两个根都是整数，写出一个满足条件的m的值，并求此时方程的两个根．

22．如图，菱形ABCD的对角线AC，BD交于点O，点E，F分别在DA，BC的延长线上，且BE⊥ED，CF=AE．
(1)求证：四边形EBFD是矩形；
(2)若AB=5，cos∠OBC=

4

5

，求BF的长．

23．在平面直角坐标系xOy中，一次函数y=-x+b的图象与x轴交于点(4，0)，且与反比例函数y=

m

x

的图象在第四象限的交点为(n，-1)．
(1)求b，m的值；
(2)点P(x_p，y_p)是一次函数y=-x+b图象上的一个动点，且满足

m

x_p

＜y_p＜4，连接OP，结合函数图象，直接写出OP长的取值范围．

24．如图，AB是⊙O的直径，CB，CD分别与⊙O相切于点B，D，连接OC，点E在AB的延长线上，延长AD，EC交于点F．
(1)求证：FA∥CO；
(2)若FA=FE，CD=4，BE=2，求FA的长．

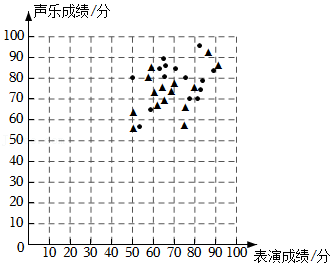
25．甲、乙两个音乐剧社各有15名学生，这两个剧社都申请报名参加某个青少年音乐剧展演活动，主办方对报名剧社的所有学生分别进行了声乐和表演两项测试，甲、乙两个剧社学生的测试成绩(百分制)统计图如下：
根据以上信息，回答下列问题：
(1)甲剧社中一名学生的声乐成绩是85分，表演成绩是60分，按声乐成绩占60%，表演成绩占40%计算学生的综合成绩，求这名学生的综合成绩；
(2)入选参加展演的剧社需要同时满足以下两个条件：首先，两项测试成绩都低于60分的人数占比不超过10%；其次，两项测试成绩中至少有一项的平均成绩不低于75分．那么乙剧社 (填“符合”或“不符合”)入选参加展演的条件；
(3)主办方计划从甲、乙两个剧社声乐和表演成绩都高于80分的学生中，随机选择两名学生参加个人展示，那么符合条件的学生一共有人，被抽选到的这两名学生分别来自不同剧社的概率是．

26．在平面直角坐标系xOy中，抛物线y=ax²+bx+c经过点(0，-2)，(2，-2)．
(1)直接写出c的值和此抛物线的对称轴；
(2)若此抛物线与直线y=-6没有公共点，求a的取值范围；
(3)点(t，y₁)，(t+1，y₂)在此抛物线上，且当-2≤t≤4时，都有|y₂-y₁|＜

7

2

．直接写出a的取值范围．

27．在△ABC中，AB=AC，过点C作射线CB'，使∠ACB'=∠ACB(点B'与点B在直线AC的异侧)点D是射线CB'上一动点(不与点C重合)，点E在线段BC上，且∠DAE+∠ACD=90°．
(1)如图1，当点E与点C重合时，AD与CB'的位置关系是，若BC=a，则CD的长为；(用含a的式子表示)
(2)如图2，当点E与点C不重合时，连接DE．
①用等式表示∠BAC与∠DAE之间的数量关系，并证明；
②用等式表示线段BE，CD，DE之间的数量关系，并证明．

28．在平面直角坐标系xOy中，对于线段AB与直线l：y=kx+b，给出如下定义：若线段AB关于直线l的对称线段为A'B'(A'，B'分别为点A，B的对应点)，则称线段A'B'为线段AB的“[k，b]关联线段”．
已知点A(1，1)，B(1，-1)．
(1)线段A'B'为线段AB的“[1，b]关联线段”，点A'的坐标为(2，0)，则A'B'的长为，b的值为；
(2)线段A'B'为线段AB的“[k，0]关联线段”，直线l₁经过点C(0，2)，若点A'，B'都在直线l₁上，连接OA'，求∠COA'的度数；
(3)点P(-3，0)，Q(-3，3)，线段A'B'为线段AB的“[k，b]关联线段”，且当b取某个值时，一定存在k使得线段A'B'与线段PQ有公共点，直接写出b的取值范围．

【2022年北京市西城区中考数学二模试卷】-第5页