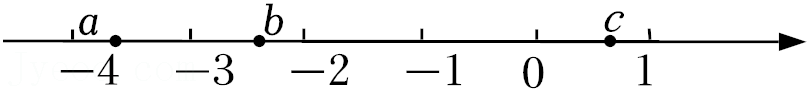
| 1 |
| m |
| m |
| m-1 |
| 1 |
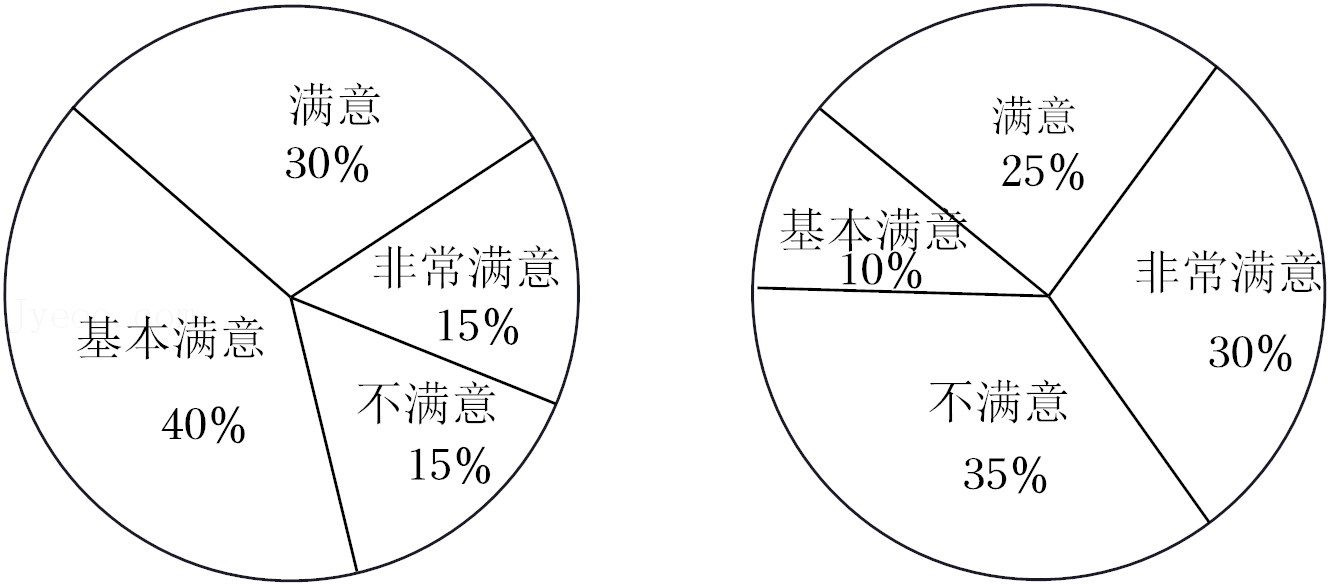
| 25 |
| 1 |
| 10 |
| 1 |
| 5 |
| 2 |
| 5 |
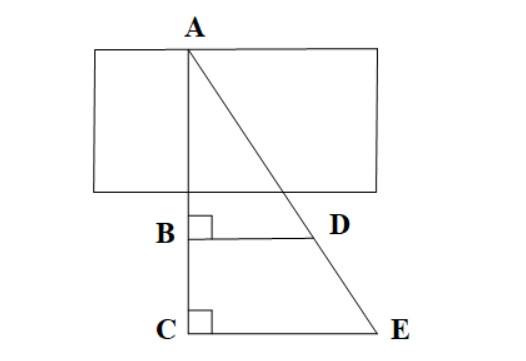
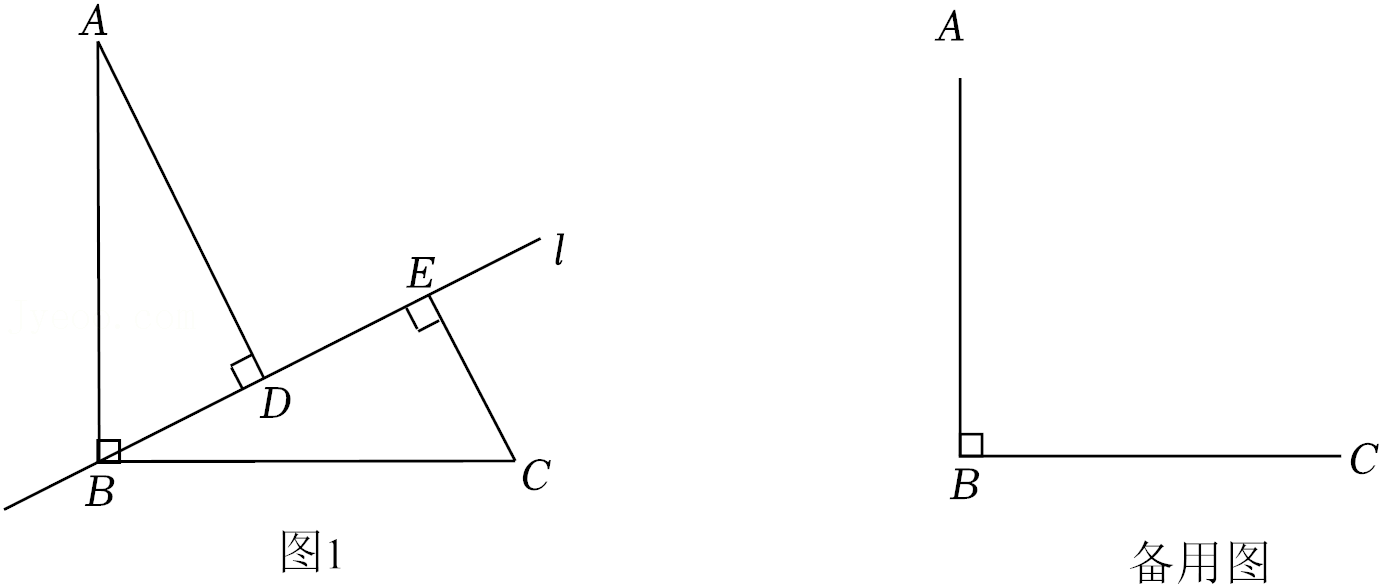
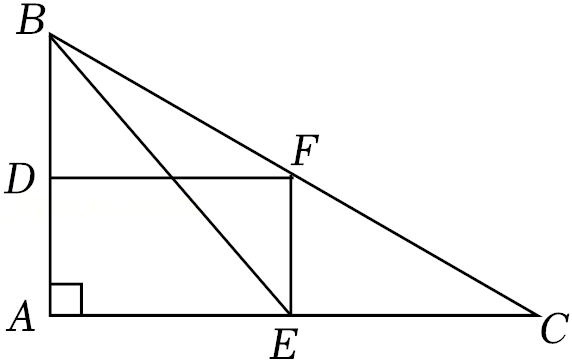
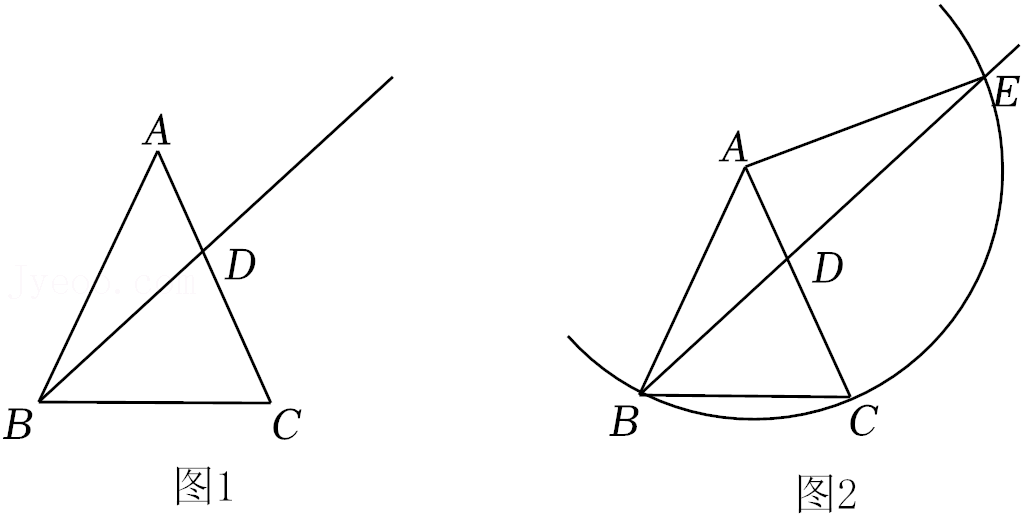
| x |
| x+BC |
| BD |
| CE |
| x |
| BC |
| BD |
| CE |
| BC |
| x+BC |
| BD |
| CE |
| BC |
| x |
| BD |
| CE |
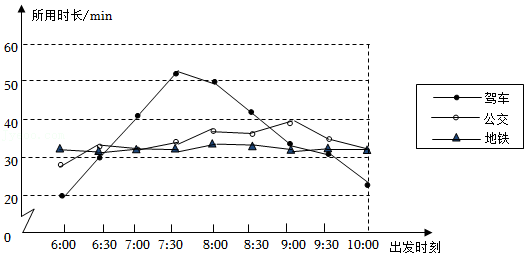
| 3 |
| x |
| 卡牌类型 | A | B | C | D | E | F |
| 数量(张) | 4 | 10 | 3 | 10 | 1 | 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| x |
| m |
| x |
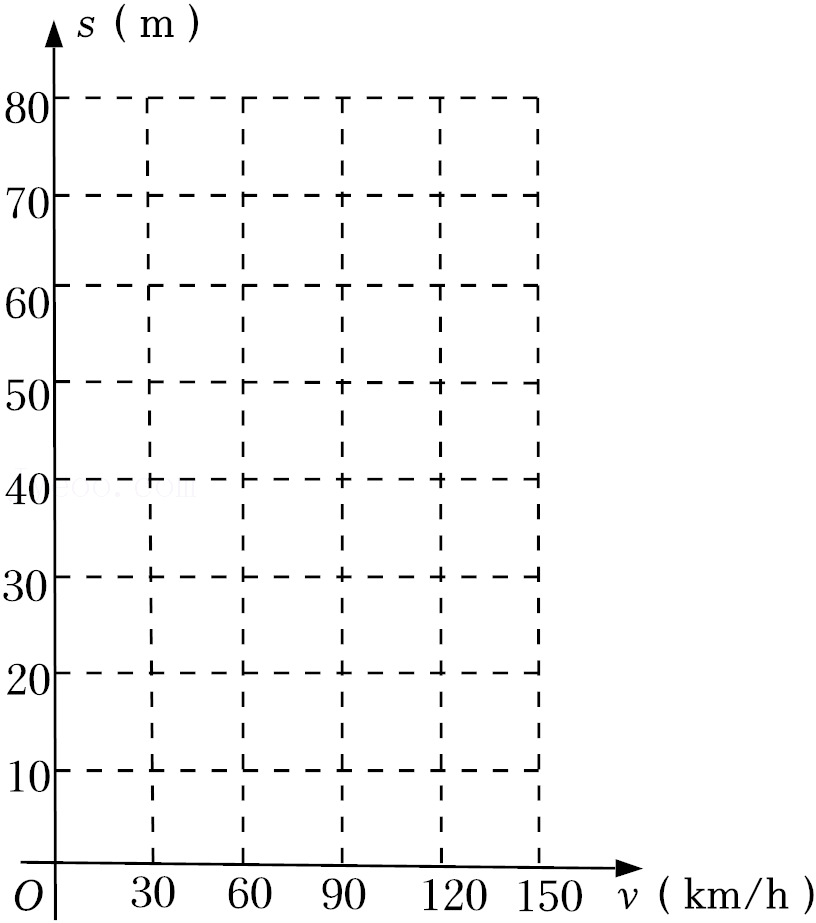
| 车速v(km/h) | 0 | 30 | 60 | 90 | 120 | 150 |
| 刹车距离s(m) | 0 | 7.8 | 19.2 | 34.2 | 52.8 | 75 |
| 款式 | 舒适性评分平均数 | 性价比评分平均数 | 时尚性评分平均数 | 综合评分平均数 |
| A | 19.5 | 19.6 | 10.2 | |
| B | 19.2 | 18.5 | 10.4 | 16.0 |
| 评分 | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x≤20 |
| 满意度 | 不满意 | 基本满意 | 满意 | 非常满意 |